
����Ŀ����ͼ����һ��������ԭ��O�͵�B������һ�£��õ�һ����������������ͼ�е�A��ʾ-10����B��ʾ10����C��ʾ18�����dzƵ�A�͵�C�����������28�����ȵ�λ������P�ӵ�A��������2��λ/����ٶ��������������������������˶����ӵ�O�˶�����B�ڼ��ٶȱ�Ϊԭ����һ�룬֮�����ָ̻�ԭ�٣�ͬʱ������Q�ӵ�C��������1��λ/����ٶ���������ĸ������˶����ӵ�B�˶�����O�ڼ��ٶȱ�Ϊԭ����������֮��Ҳ���ָ̻�ԭ�٣����˶���ʱ��Ϊt�룬�ʣ�
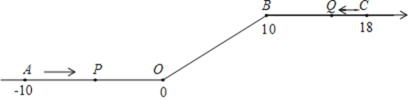
��1������P�ӵ�A�˶�����C��Ҫ________�룻
��2��P��Q��������ʱ�����������M����Ӧ�����Ƕ��٣�
��3����tΪ��ֵʱ��P��O���������������ij�����Q��B���������������ij������.
���𰸡���1��19�룻��2��������M����Ӧ������![]() ����3��t��ֵΪ2��6.5��11��17
����3��t��ֵΪ2��6.5��11��17
��������
��1������·�̳����ٶȵ���ʱ�䣬�ɵô𰸣�
��2����������ʱP��Q�˶���ʱ����ȣ��ɵ÷��̣��ⷽ�̣��ɵô𰸣�
��3������PO��BQ��ȣ��ɵ÷��̣��ⷽ�̣��ɵô𰸣�
�⣺��1����P�˶�����Cʱ������ʱ��t=![]() ���룩��
���룩��
��2�������֪��P��Q�����������߶�OB����M������OM=![]() ��
��
��![]() ��
��
���![]() ����������M����Ӧ������
����������M����Ӧ������![]() ��
��
��3��P��O���������������ij�����Q��B���������������ij��������4�ֿ��ܣ�
�ٶ���Q��CB�ϣ�����P��AO�ϣ���8-t=10-2t����ã�t=2��
�ڶ���Q��CB�ϣ�����P��OB�ϣ���8-t=��t-5����1����ã�t=6.5��
�۶���Q��BO�ϣ�����P��OB�ϣ���2��t-8��=��t-5����1����ã�t=11��
�ܶ���Q��OA�ϣ�����P��BC�ϣ���10+2��t-15��=t-13+10����ã�t=17��
����������t��ֵΪ2��6.5��11��17��


 ÿ��10���ӿ�����������������ϵ�д�
ÿ��10���ӿ�����������������ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��һ�κ���y��x��m��ͼ���뷴��������y��![]() ��ͼ����A��B���㣬����x�ύ�ڵ�C����A������Ϊ(2��1)��
��ͼ����A��B���㣬����x�ύ�ڵ�C����A������Ϊ(2��1)��
(1)��m��k��ֵ��
(2)���C�����꣬�����ͼ��д������ʽ��0��x��m��![]() �Ľ⼯��
�Ľ⼯��

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�������и���������Ӧ�Ĵ������ڣ�
0.275����|��2|����1.04��������10��2��������8��, -![]() ��0����
��0����![]() .
.
��������{���� ��}��
�Ǹ���������{���� ��}��
��������{���� ��}��
��������{���� ��}��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���۲����н�����̣�
���㣺1+5+52+53+��+524+525��ֵ��
�⣺��S=1+5+52+53+��+524+525����1��
��5S=5+52+53+��+525+526��2��
��2������1������4S=526��1
S=![]()
ͨ���Ķ�����һ��ѧ����һ�ֽ������ķ�����������ѧ���ķ������㣺
��1��1+3+32+33+��+39+310
��2��1+x+x2+x3+��+x99+x100��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ijУ��չ�������ݳǣ�����ͬ�С��Ļ������ѧ������˫������亽����μ���ѡ���Ϊ���˽�ͬѧ���Ͷ�ʱ�䣬ѧУ��������˲���ͬѧ�Ͷ���ʱ�䣬���õõ������ݻ����˲�������ͳ��ͼ������ͼ����Ϣ����������⣺
��1��������ͳ��ͼ����������
��2������ѧ���Ͷ�ʱ�������Ϊ______����λ��Ϊ_______��
��3����֪ȫУѧ������Ϊ1200�ˣ�������Уѧ���μ������Ͷ�2Сʱ���ж����ˣ�

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ������̽������֪��ֽ������һ����(��ͼ��ʾ)��
![]()
(1)�۵�ֽ�棬ʹ��ʾ�ĵ�1�룭1�غϣ���2��ʾ�ĵ��� �� ��ʾ�ĵ��غϣ�
(2)�۵�ֽ�棬ʹ��1��ʾ�ĵ���3��ʾ�ĵ��غϣ��ش��������⣺
�� 5��ʾ�ĵ����� �� ��ʾ�ĵ��غϣ�
��![]() ��ʾ�ĵ����� �� ��ʾ�ĵ��غϣ�
��ʾ�ĵ����� �� ��ʾ�ĵ��غϣ�
����������A��B����֮�����Ϊ9(A��B�����)����A��B���㾭�۵����غϣ���ʱ��A��ʾ������ �� ����B��ʾ������ �� .
(3)��֪�������ϵ�A��ʾ������a����A�ƶ�4����λ����ʱ��A��ʾ������a�ǻ�Ϊ�෴������a��ֵ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ�������ϣ���A�ij�ʼλ�ñ�ʾ����Ϊ1���ֵ�A�������ƶ�����1�ε�A�����ƶ�3����λ��������![]() ����2�δӵ�
����2�δӵ�![]() �����ƶ�6����λ��������
�����ƶ�6����λ��������![]() ����3�δӵ�
����3�δӵ�![]() �����ƶ�9����λ��������
�����ƶ�9����λ��������![]() ���������������ƶ���ʽ������ȥ�������
���������������ƶ���ʽ������ȥ�������![]() ��ԭ��ľ��벻С��20����ôn����Сֵ��________��
��ԭ��ľ��벻С��20����ôn����Сֵ��________��
![]()
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
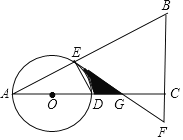
����Ŀ����ͼ������ABC�У���ACB=90�㣬O�DZ�AC��һ�㣬��OΪԲ�ģ�OAΪ�뾶��Բ�ֱ�AB��AC�ڵ�E��D����BC���ӳ�����ȡ��F��ʹ��BF=EF��EF��AC���ڵ�G��
��1�����ж�ֱ��EF����O��λ�ù�ϵ����˵�����ɣ�
��2����OA=2����A=30�㣬��ͼ����Ӱ���ֵ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪��b����С������������a��b���㣨c��5��2+|a+b|=0��
![]()
��1�������a��b��c��ֵ��
��2��a��b��c����Ӧ�ĵ�ֱ�ΪA��B��C����PΪһ���㣬���Ӧ����Ϊx����P��0��2֮���˶�ʱ����0��x��2ʱ�����뻯��ʽ�ӣ�|x+1|-|x-1|+2|x+5|����д��������̣�
��3���ڣ�1����2���������£���A��B��C��ʼ���������˶�������A��ÿ��1����λ���ȵ��ٶ������˶���ͬʱ����B�͵�C�ֱ���ÿ��2����λ���Ⱥ�5����λ���ȵ��ٶ������˶�������t���ӹ�������B���C֮��ľ����ʾΪBC����A���B֮��ľ����ʾΪAB�����ʣ�BC-AB��ֵ�Ƿ�����ʱ��t�ı仯���ı䣿���仯����˵�����ɣ������䣬������ֵ��
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com