
如图,在平面直角坐标系的第一象限中,有一各边所在直线均平行于坐标轴的矩形ABCD,且点A在反比例函数L1:y=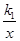 (x>0) 的图象上,点C在反比例函数L2:y=
(x>0) 的图象上,点C在反比例函数L2:y=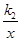 (x>0) 的图象上(矩形ABCD夹在L1与L2之间).(1)若点A坐标为(1,1)时,则L1的解析式为 .(2)在(1)的条件下,若矩形ABCD是边长为1的正方形,求L2的解析式.(3)若k1=1,k2=6,且矩形ABCD的相邻两边分别为1和2,求符合条件的顶点C的坐标.
(x>0) 的图象上(矩形ABCD夹在L1与L2之间).(1)若点A坐标为(1,1)时,则L1的解析式为 .(2)在(1)的条件下,若矩形ABCD是边长为1的正方形,求L2的解析式.(3)若k1=1,k2=6,且矩形ABCD的相邻两边分别为1和2,求符合条件的顶点C的坐标.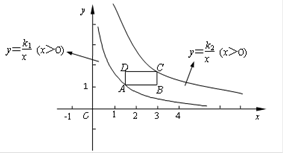
(1)y=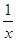 (x>0);(2)y=
(x>0);(2)y= 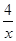 (x>0);符合题意的点C的坐标为(4,
(x>0);符合题意的点C的坐标为(4,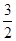 )或(3,2)或(
)或(3,2)或(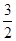 ,4)或(2,3).
,4)或(2,3).
解析试题分析:(1)点A(1,1)在反比例函数y= 上,则将x=1,y=1代入反比例函数式中,等式一定成立,所以有k1=1.(2)根据题意,将点A向右平移1个单位,再向上平移1个单位,就得到点C,所以点C的坐标是(2,2),将点C(2,2)代入反比例函数y=
上,则将x=1,y=1代入反比例函数式中,等式一定成立,所以有k1=1.(2)根据题意,将点A向右平移1个单位,再向上平移1个单位,就得到点C,所以点C的坐标是(2,2),将点C(2,2)代入反比例函数y=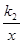 得k2=4.(3)设点A的横坐标是a,则纵坐标是
得k2=4.(3)设点A的横坐标是a,则纵坐标是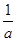 ,分两种情况讨论:当AB=1,AD=2时,此时,点C的坐标应为(a+1,
,分两种情况讨论:当AB=1,AD=2时,此时,点C的坐标应为(a+1, 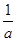 +2),代入直线L2的关系式中,即可求得点C的坐标;当AB=2,AD=1时,点C的坐标可表示为(a+2,
+2),代入直线L2的关系式中,即可求得点C的坐标;当AB=2,AD=1时,点C的坐标可表示为(a+2, 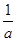 +1),代入直线L2的表达式中,就可求得点C的坐标.
+1),代入直线L2的表达式中,就可求得点C的坐标.
试题解析:(1)y=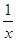 (x>0);(2)y=
(x>0);(2)y=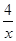 (x>0)
(x>0)
(3)①当AB=1,AD=2时,设A点坐标为(a,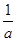 ),则C点坐标为(a+1,
),则C点坐标为(a+1, 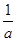 +2),
+2),
由已知有(a+1)(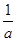 +2)=6,解得a=1或a=
+2)=6,解得a=1或a=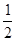
故此时符合条件的C点有(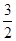 ,4)和(2,3)
,4)和(2,3)
②当AB=2,AD=1时,设A点坐标为(a,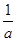 ),则C点坐标为(a+2,
),则C点坐标为(a+2,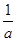 +1),
+1),
由已知有(a+2)(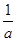 +1)=6,解得a=1或a=2
+1)=6,解得a=1或a=2
故此时符合条件的C点有(4,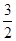 )和(3,2)
)和(3,2)
综上所述,符合题意的点C的坐标为(4,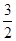 )或(3,2)或(
)或(3,2)或(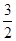 ,4)或(2,3).
,4)或(2,3).
考点:反比例函数的图象


科目:初中数学 来源: 题型:解答题
已知y=y1-y2,其中y1是x的反比例函数,y2是x2的正比例函数,且x=1时y=3,x=-2时y=-15.
求:(1)y与x之间的函数关系式;
(2)当x=2时y的值.
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
(1)先求解下列两题: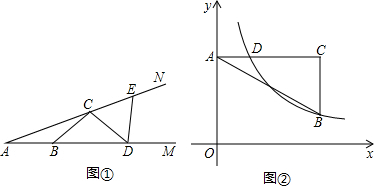
①如图①,点B,D在射线AM上,点C,E在射线AN上,且AB=BC=CD=DE,已知∠EDM=84°,求∠A的度数;
②如图②,在直角坐标系中,点A在y轴正半轴上,AC∥x轴,点B,C的横坐标都是3,且BC=2,点D在AC上,且横坐标为1,若反比例函数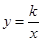 (x>0)的图象经过点B,D,求k的值.
(x>0)的图象经过点B,D,求k的值.
(2)解题后,你发现以上两小题有什么共同点?请简单地写出.
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
如图,科技小组准备用材料围建一个面积为60m2的矩形科技园ABCD,其中一边AB靠墙,墙长为12m,设AD的长为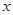 m,DC的长为
m,DC的长为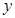 m.
m.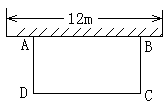
(1)求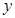 与
与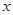 之间的函数关系式;
之间的函数关系式;
(2)若围成矩形科技园ABCD的三边材料总长不超过26m,材料AD和DC的长都是整米数,求出满足条件的所有围建方案.
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
如图,一次函数的图象与x轴,y轴分别相交于A,B两点,且与反比例函数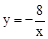 的图象在第二象限交与点C,如果点A为的坐标为(2,0),B是AC的中点.
的图象在第二象限交与点C,如果点A为的坐标为(2,0),B是AC的中点.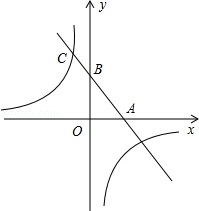
(1)求点C的坐标;
(2)求一次函数的解析式.
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
如图,在平面直角坐标系xOy中,一次函数y=kx+b与反比例函数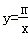 的图象交于点A,与x轴交于点B,AC⊥x轴于点C,
的图象交于点A,与x轴交于点B,AC⊥x轴于点C,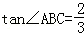 ,AB=
,AB=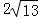 ,OB=OC.
,OB=OC.
(1)求反比例函数和一次函数的解析式;
(2)若一次函数与反比例函数的图象的另一交点为D,作DE⊥y轴于点E,连接OD,求△DOE的面积.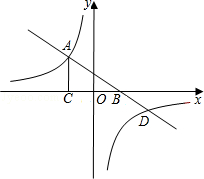
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com