
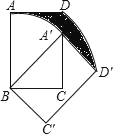
【题目】如图,在矩形ABCD中AB=![]() ,BC=1,将矩形ABCD绕顶点B旋转得到矩形A'BC'D,点A恰好落在矩形ABCD的边CD上,则AD扫过的部分(即阴影部分)面积为( )
,BC=1,将矩形ABCD绕顶点B旋转得到矩形A'BC'D,点A恰好落在矩形ABCD的边CD上,则AD扫过的部分(即阴影部分)面积为( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
 黄冈小状元解决问题天天练系列答案
黄冈小状元解决问题天天练系列答案 三点一测快乐周计划系列答案
三点一测快乐周计划系列答案科目:初中数学 来源: 题型:
【题目】某家具商场计划购进某种餐桌、餐椅进行销售,有关信息如表:
原进价(元/张) | 零售价(元/张) | 成套售价(元/套) | |
餐桌 | a | 270 | 500元 |
餐椅 | a﹣110 | 70 |
已知用600元购进的餐桌数量与用160元购进的餐椅数量相同.
(1)求表中a的值;
(2)若该商场购进餐椅的数量是餐桌数量的5倍还多20张,且餐桌和餐椅的总数量不超过200张.该商场计划将一半的餐桌成套(一张餐桌和四张餐椅配成一套)销售,其余餐桌、餐椅以零售方式销售.请问怎样进货,才能获得最大利润?最大利润是多少?
(3)由于原材料价格上涨,每张餐桌和餐椅的进价都上涨了10元,但销售价格保持不变.商场购进了餐桌和餐椅共200张,应怎样安排成套销售的销售量(至少10套以上),使得实际全部售出后,最大利润与(2)中相同?请求出进货方案和销售方案.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:△ABC内接于⊙O,连接CO并延长交AB于点E,交⊙O于点D,满足∠BEC=3∠ACD.
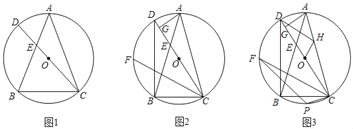
(1)如图1,求证:AB=AC;
(2)如图2,连接BD,点F为弧BD上一点,连接CF,弧CF=弧BD,过点A作AG⊥CD,垂足为点G,求证:CF+DG=CG;
(3)如图3,在(2)的条件下,点H为AC上一点,分别连接DH,OH,OH⊥DH,过点C作CP⊥AC,交⊙O于点P,OH:CP=1:![]() ,CF=12,连接PF,求PF的长.
,CF=12,连接PF,求PF的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在![]() 中
中![]() ,点
,点![]() ,
,![]() 分别为
分别为![]() ,
,![]() 的中点,连接
的中点,连接![]() ,作
,作![]() 与
与![]() 相切于点
相切于点![]() ,在
,在![]() 边上取一点
边上取一点![]() ,使
,使![]() ,连接
,连接![]() .
.
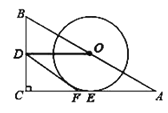
(1)判断直线![]() 与
与![]() 的位置关系,并说明理由;
的位置关系,并说明理由;
(2)当![]() ,
,![]() 时,求
时,求![]() 的半径.
的半径.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知关于x的方程x2-(m+2)x+(2m-1)=0。
(1)求证:方程恒有两个不相等的实数根;
(2)若此方程的一个根是1,请求出方程的另一个根,并求以此两根为边长的直角三角形的周长。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下图为某区域部分交通线路图,其中直线![]() ,直线
,直线![]() 与直线
与直线![]() 都垂直,,垂足分别为点A、点B和点C,(高速路右侧边缘),
都垂直,,垂足分别为点A、点B和点C,(高速路右侧边缘),![]() 上的点M位于点A的北偏东30°方向上,且BM=
上的点M位于点A的北偏东30°方向上,且BM=![]() 千米,
千米,![]() 上的点N位于点M的北偏东
上的点N位于点M的北偏东![]() 方向上,且
方向上,且![]() ,MN=
,MN=![]() 千米,点A和点N是城际线L上的两个相邻的站点.
千米,点A和点N是城际线L上的两个相邻的站点.
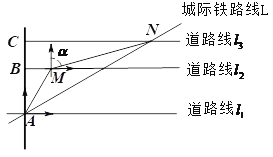
(1)求![]() 之间的距离
之间的距离
(2)若城际火车平均时速为150千米/小时,求市民小强乘坐城际火车从站点A到站点N需要多少小时?(结果用分数表示)
查看答案和解析>>
科目:初中数学 来源: 题型:
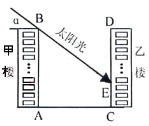
【题目】下图为某小区的两幢1O层住宅楼,由地面向上依次为第1层、第2层、…、第10层,每层的高度为3m,两楼间的距离AC=30m.现需了解在某一时段内,甲楼对乙楼的采光的影响情况.假设某一时刻甲楼楼顶B落在乙楼的影子长EC=h,太阳光线与水平线的夹角为α.
(1)用含α的式子表示h;
(2)当α=30°时,甲楼楼顶B的影子落在乙楼的第几层?从此时算起,若α每小时增加10°,几小时后,甲楼的影子刚好不影响乙楼采光.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点E在△ABC的边AB上,过点B,C,E的⊙O切AC于点C.直径CD交BE于点F,连结BD,DE.已知∠A=∠CDE,AC=2![]() ,BD=1.
,BD=1.
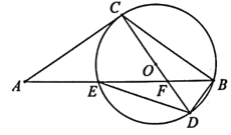
(1)求⊙O的直径.
(2)过点F作FG⊥CD交BC于点G,求FG的长.
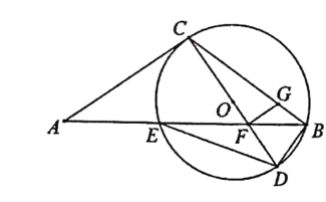
查看答案和解析>>
科目:初中数学 来源: 题型:
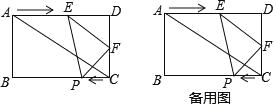
【题目】如图,在矩形 ABCD 中,AB=6cm,AD=8cm,直线 EF 从点 A 出发沿 AD 方向匀速运动,速度是 2cm/s,运动过程中始终保持 EF∥AC.F 交
AD 于 E,交 DC 于点 F;同时,点 P 从点 C 出发沿 CB 方向匀速运动,速度是 1cm/s,连接 PE、PF,设运动时间 t(s)(0<t<4).
(1)当 t=1 时,求 EF 长;
(2)求 t 为何值时,四边形 EPCD 为矩形;
(3)设△PEF 的面积为 S(cm2),求出面积 S 关于时间 t 的表达式;
(4)在运动过程中,是否存在某一时刻使 S△PC F:S 矩形 ABCD=3:16?若存在, 求出 t 的值;若不存在,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com