
【题目】为了鼓励节能降耗,某市规定如下用电收费标准:每户每月的用电量不超过120度时,电价为a元/度;超过120度时,不超过部分仍为a元/度,超过部分为b元/度.已知某用户五月份用电115度,交电费69元,六月份用电140度,交电费94元.
(1)求a,b的值;
(2)设该用户每月用电量为x(度),应付电费为y(元);
①分别求出0≤x≤120和x>120时,y与x之间的函数关系式;
②若该用户计划七月份所付电费不超过83元,问该用户七月份最多可用电多少度?
【答案】(1)![]() ;(2)①当0≤x≤120时,y=0.6x;当x>120时y=1.1x﹣60;②该用户七月份最多可用电130度
;(2)①当0≤x≤120时,y=0.6x;当x>120时y=1.1x﹣60;②该用户七月份最多可用电130度
【解析】
(1)先根据“五月份用电115度,交电费69元”“六月份用电140度,交电费94元”作为相等关系列方程组解出a,b的值;
(2)根据(1)中所求数值得到当0≤x≤120时,y=0.6x;当x>120时y=1.1x﹣60.根据题意可求解.
解:(1)根据题意,得![]() ,
,
解这个方程组,得![]() ;
;
(2)①当0≤x≤120时,y=0.6x,
当x>120时,y=120×0.6+1.1(x﹣120),即y=1.1x﹣60;
②∵83>120×0.6=72,
∴y与x之间的函数关系式为y=1.1x﹣60,
由题意得1.1x﹣60≤83,
∴x≤130.
∴该用户七月份最多可用电130度.


科目:初中数学 来源: 题型:
【题目】如图,Rt△ABO的顶点A是反比例函数y=![]() 与一次函数y=﹣x﹣(k+1)的图象在第二象限的交点,AB⊥x轴于B,且S△ABO=
与一次函数y=﹣x﹣(k+1)的图象在第二象限的交点,AB⊥x轴于B,且S△ABO=![]() .
.
(1)直接写出这两个函数的关系式;
(2)求△AOC的面积;
(3)根据图象直接写出:当x为何值时,反比例函数的值小于一次函数的值.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,二次函数y=ax2+bx+c(a≠0)的图象与x轴交于A,B两点,与y轴交于点C,且OA=OC.则下列结论:①abc<0;②![]() >0;③ac-b+1=0;④OA·OB=-
>0;③ac-b+1=0;④OA·OB=-![]() .其中结论正确的是____________
.其中结论正确的是____________
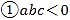
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系![]() 中,正方形ABCD的顶点分别为A(0,1),B(-1,0),C(0,-1),D(1,0).对于图形M,给出如下定义:P为图形M上任意一点,Q为正方形ABCD边上任意一点,如果P,Q两点间的距离有最大值,那么称这个最大值为图形M的“正方距”,记作
中,正方形ABCD的顶点分别为A(0,1),B(-1,0),C(0,-1),D(1,0).对于图形M,给出如下定义:P为图形M上任意一点,Q为正方形ABCD边上任意一点,如果P,Q两点间的距离有最大值,那么称这个最大值为图形M的“正方距”,记作![]() .
.
(1)已知点![]() ,
,
①直接写出![]() 的值;
的值;
②直线![]() 与x轴交于点F,当
与x轴交于点F,当![]() 取最小值时,求k的取值范围;
取最小值时,求k的取值范围;
(2)![]() 的圆心为
的圆心为![]() ,半径为1.若
,半径为1.若![]() ,直接写出t的取值范围.
,直接写出t的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在一个不透明的盒子中装有大小和形状相同的3个红球和2个白球,把它们充分搅匀.
(1)求从中任意抽取1个球恰好是红球的概率;
(2)学校决定在甲、乙两名同学中选取一名作为学生代表发言,制定如下规则:从盒子中任取两个球,若两球同色,则选甲;若两球异色,则选乙,你认为这个规则公平吗?请用列表法或画树状图法加以说明.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了测量一个铁球的直径,将该铁球放入工件槽内,测得的有关数据如图所示(单位:cm),则该铁球的直径为( )
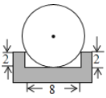
A.12 cmB.10 cmC.8 cmD.6 cm
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在直角三角形中,除直角外的5个元素中,已知2个元素(其中至少有1个是边),就可以求出其余的3个未知元素.对于任意三角形,我们需要知道几个元素就可以求出其余的未知元素呢?思考并解答下列问题:
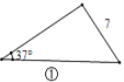

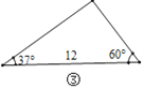
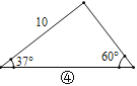
(1)观察图①~图④,根据图中三角形的已知元素,可以求出其余未知元素的序号是____.
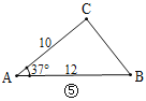
(2)如图⑤,在![]() 中,已知
中,已知![]() ,
,![]() ,
,![]() ,能否求出BC的长度?如果能,请求出BC的长度;如果不能,请说明理由.(参考数据:
,能否求出BC的长度?如果能,请求出BC的长度;如果不能,请说明理由.(参考数据:![]() ,
,![]() ,
,![]() )
)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系xOy中,函数![]() 的图象G经过点
的图象G经过点![]() ,直线
,直线![]() 与y轴交于点B,与图象G交于点C.
与y轴交于点B,与图象G交于点C.
(1)求m的值.
(2)横、纵坐标都是整数的点叫做整点.记图象G在点A,C之间的部分与线段BA,BC围成的区域(不含边界)为W.
①当直线l过点![]() 时,直接写出区域W内的整点个数.
时,直接写出区域W内的整点个数.
②若区域W内的整点不少于4个,结合函数图象,求k的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】水务部门为加强防汛工作,决定对马边河上某电站大坝进行加固.原大坝的横断面是梯形ABCD,如图所示,已知迎水面AB的长为20米,∠B=60°,背水面DC的长度为20![]() 米,加固后大坝的横断面为梯形ABED.若CE的长为5米.
米,加固后大坝的横断面为梯形ABED.若CE的长为5米.
(1)已知需加固的大坝长为100米,求需要填方多少立方米;
(2)求新大坝背水面DE的坡度.(计算结果保留根号).
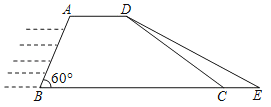
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com