
 如图,抛物线y=a(x-1)2+4与x轴交于点A,B,与y轴交于点C,过点C作CD∥x轴交抛物线的对称轴于点D,连接BD,已知点A的坐标为(-1,0)
如图,抛物线y=a(x-1)2+4与x轴交于点A,B,与y轴交于点C,过点C作CD∥x轴交抛物线的对称轴于点D,连接BD,已知点A的坐标为(-1,0)分析 (1)将A坐标代入抛物线解析式,求出a的值,即可确定出解析式;
(2)抛物线解析式令x=0求出y的值,求出OC的长,根据对称轴求出CD的长,令y=0求出x的值,确定出OB的长,利用梯形面积公式即可求出梯形COBD的面积;
(3)过点P作y轴的平行线,交直线BC于点F,用未知数设出点P、F的坐标,即可得到线段PF的长度表达式,以PF为底、C到B的水平距离为高,即可得到△PBC的面积函数关系式,根据函数的性质即可求出△PBC的面积最大时,点P的坐标.
解答 解:(1)将A(-1,0)代入y=a(x-1)2+4中,得:0=4a+4,
解得:a=-1,
则抛物线解析式为y=-(x-1)2+4;
(2)对于抛物线解析式,令x=0,得到y=3,即OC=3,
∵抛物线解析式为y=-(x-1)2+4的对称轴为直线x=1,
∴CD=1,
∵A(-1,0),
∴B(3,0),即OB=3,
则S梯形COBD=$\frac{(1+3)×3}{2}$=6;
(3)y=-(x-1)2+4=-x2+2x+3.
∵B(3,0),(0,3),
∴易得直线BC的解析式为:y=-x+3.
如图,点P作y轴的平行线,交直线BC于点F,
设P(m,-m2+2m+3),则F(m,-m+3),
∴PF=-m2+2m+3+m-3=-m2+3m.
∴S△PBC=$\frac{1}{2}$PF•OB=$\frac{1}{2}$(-m2+3m)×3=-$\frac{3}{2}$(m-$\frac{3}{2}$)2+$\frac{27}{8}$.
故当m=$\frac{3}{2}$时,△PBC的面积最大,此时P($\frac{3}{2}$,$\frac{15}{4}$).
点评 本题主要考查了二次函数综合题,此题涉及到待定系数法求函数解析式,二次函数的性质、三角形面积的计算、梯形面积的求法等知识,解答(3)问关键是求出PF的长,利用三角形的面积公式和二次函数最值的求法进行解答,此题有一定的难度.


科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源:2017届江苏省盐都市九年级下学期第一次学情调研数学试卷(解析版) 题型:判断题
(本题满分10分)
一汽车租赁公司拥有某种型号的汽车100辆.公司在经营中发现每辆车的月租金
x(元)与每月租出的车辆数(y)有如下关系:
x | 4500 | 4000 | 3800 | 3200 |
y | 70 | 80 | 84 | 96 |
(1)观察表格,用所学过的一次函数、反比例函数或二次函数的有关知识求出每月租出的车辆数y(辆)与每辆车的月租金x(元)之间的关系式.
(2)已知租出的车每辆每月需要维护费150元,未租出的车每辆每月需要维护费50元. 每辆车的月租金定为多少元时,才能使公司获得最大月收益?请求出公司的最大月收益是多少元.
查看答案和解析>>
科目:初中数学 来源:2017届江苏省盐都市九年级下学期第一次学情调研数学试卷(解析版) 题型:单选题
在△ABC中,AB=3,AC=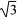 . 当∠B最大时,BC的长是( )
. 当∠B最大时,BC的长是( )
A. 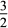 B.
B.  C.
C.  D. 2
D. 2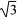
查看答案和解析>>
科目:初中数学 来源:2017届江苏省盐都市九年级下学期第一次学情调研数学试卷(解析版) 题型:单选题
在-2、0、1、2这四个数中,最小的数是( )
A. -2 B. 0 C. 1 D. 2
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 有一个角为40°的两个等腰三角形 | |
| B. | 两个直角三角形 | |
| C. | 两条边对应成比例,一个对应角相等的两个三角形 | |
| D. | 有一个角为100°的两个等腰三角形 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com