
【题目】如图,矩形EFGH的顶点E,G分别在菱形ABCD的边AD,BC上,顶点F,H在菱形ABCD的对角线BD上.

(1)求证:BG=DE;
(2)若E为AD中点,FH=2,求菱形ABCD的周长.
科目:初中数学 来源: 题型:
【题目】下列四个函数:
①y=kx(k为常数,k>0)
②y=kx+b(k,b为常数,k>0)
③y=![]() (k为常数,k>0,x>0)
(k为常数,k>0,x>0)
④y=ax2(a为常数,a>0)
其中,函数y的值随着x值得增大而减少的是( )
A. ① B. ② C. ③ D. ④
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】先化简,再求值![]() ,其中
,其中![]() 的值从不等式组
的值从不等式组![]() 的整数解中选取.
的整数解中选取.
【答案】(a-2)2.
【解析】试题分析:根据分式的减法和除法可以化简题目中的式子,然后在不等式组![]() 的解集中选取一个使得原分式有意义的整数值代入化简后的式子即可解答本题.
的解集中选取一个使得原分式有意义的整数值代入化简后的式子即可解答本题.
试题解析:
解:原式=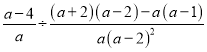
=![]()
=![]()
=(a-2)2,
由不等式组![]() 得,0≤a<5.5,
得,0≤a<5.5,
∴当a=1时,原式=(1-2)2=1.
点睛:本题考查分式的化简求值、一元一次不等式组的整数解,解答本题的关键是明确分式化简求值的方法,会求一元一次不等式组的解集.
【题型】解答题
【结束】
22
【题目】某校为了开展读书月活动,对学生最喜欢的图书种类进行了一次抽样调查,所有图书分成四类:艺术、文学、科普、其他.随机调查了该校m名学生(每名学生必选且只能选择一类图书),并将调查结果制成如下两幅不完整的统计图:
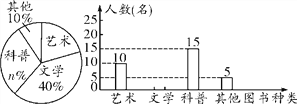
根据统计图提供的信息,解答下列问题:
(1)m= ,n= ;
(2)扇形统计图中,“艺术”所对应的扇形的圆心角度数是 度;
(3)请根据以上信息补全条形统计图;
(4)根据抽样调查的结果,请你估计该校1000名学生中有多少学生最喜欢科普类图书.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】用图1中四个完全一样的直角三角形可以拼成图2的大正方形。

解答下列问题:
(1)请用含![]() 、
、![]() 、
、![]() 的代数式表示大正方形的面积.
的代数式表示大正方形的面积.
方法1: ;方法2: .
(2)根据图2,利用图形的面积关系,推导![]() 、
、![]() 、
、![]() 之间满足的关系式.
之间满足的关系式.
(3)利用(2)的关系式解答:如果大正方形的面积是25,且![]() ,求小正方形的面积.
,求小正方形的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小明外出游玩时,带了![]() 件上衣和
件上衣和![]() 条长裤,上衣颜色有白色、蓝色,长裤有白色、黑色、蓝色,随意拿出一条裤子和一件上衣问题为:
条长裤,上衣颜色有白色、蓝色,长裤有白色、黑色、蓝色,随意拿出一条裤子和一件上衣问题为:
(![]() )小明随意拿出一条裤子和一件上衣配成一套,列出所有可能出现结果的“树状图”;
)小明随意拿出一条裤子和一件上衣配成一套,列出所有可能出现结果的“树状图”;
(![]() )他任意拿出一件上衣和一条长裤穿上的颜色正好相同的概率是多少?
)他任意拿出一件上衣和一条长裤穿上的颜色正好相同的概率是多少?
(![]() )小明正好拿出黑色长裤的概率是多少?
)小明正好拿出黑色长裤的概率是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知,抛物线![]() ( a≠0)经过原点,顶点为A(h,k)(h≠0).
( a≠0)经过原点,顶点为A(h,k)(h≠0).
(1)当h=1,k=2时,求抛物线的解析式;
(2)若抛物线![]() (t≠0)也经过A点,求a与t之间的关系式;
(t≠0)也经过A点,求a与t之间的关系式;
(3)当点A在抛物线![]() 上,且-2≤h<1时,求a的取值范围.
上,且-2≤h<1时,求a的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图:在平行四边形ABCD中,用直尺和圆规作∠BAD的平分线交BC于点E(尺规作图的痕迹保留在图中了),连接EF.
(1)求证:四边形ABEF为菱形;
(2)AE,BF相交于点O,若BF=6,AB=5,求AE的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,P为正方形ABCD的边BC上一动点(P与B、C不重合),连接AP,过点B作BQ⊥AP交CD于点Q,将△BQC沿BQ所在的直线对折得到△BQC′,延长QC′交BA的延长线于点M.
(1)试探究AP与BQ的数量关系,并证明你的结论;
(2)当AB=3,BP=2PC,求QM的长;
(3)当BP=m,PC=n时,求AM的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】矩形![]() 的对角线交于点
的对角线交于点![]() ,
,![]() .
.
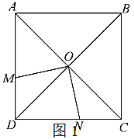
(1)如图1,![]() ,
,![]() ,点
,点![]() 在边
在边![]() 上,点
上,点![]() 在边
在边![]() 上,求证:
上,求证:![]() ;
;
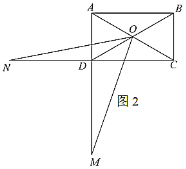
(2)如图2,![]() ,
,![]() ,点
,点![]() 在线段
在线段![]() 的延长线上,点
的延长线上,点![]() 在线段
在线段![]() 的延长线上,若
的延长线上,若![]() ,求
,求![]() 的值;
的值;
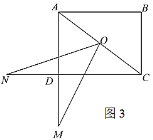
(3)如图3,![]() ,
,![]() ,
,![]() ,点
,点![]() 在线段
在线段![]() 的延长线上,点
的延长线上,点![]() 在线段
在线段![]() 的延长线上,若
的延长线上,若![]() ,直接写出线段
,直接写出线段![]() 的长度.
的长度.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com