
【题目】东方红中学位于东西方向的一条路上,一天我们学校的李老师出校门去家访,他先向西走100米到聪聪家,再向东走150米到青青家,再向西走200米到刚刚家,请问:
(1)如果把这条路看作一条数轴,以向东为正方向,以校门口为原点,请你在这条数轴上标出聪聪家与青青家的大概位置(数轴上一格表示50米).
(2)聪聪家与刚刚家相距多远?
(3)聪聪家向西20米所表示的数是多少?
![]()
 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:
【题目】在“端午节”期间,小明、小亮等同学随家长一行共12人到某公园游玩,成人门票每张40元,学生门票5折优惠,小明直接去窗口买票需要400元.
(1)他们共去了几个成人,几个学生?
(2)小亮从美团网看到订团体票信息,9人以上(含9人)的团体订票按成人价8.5折优惠,请你帮助策划,用何种方式购票最省钱,给出方案并计算出票价总数?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】决心试一试,请阅读下列材料:计算:![]()
解法一:原式=![]()
=![]()
=![]()
解法二:原式=![]()
=![]()
=![]()
=![]()
解法三:原式的倒数为:![]()
=![]()
=﹣20+3﹣5+12
=﹣10
故原式 =![]()
上述得出的结果不同,肯定有错误的解法,你认为解法 是错误的,在正确的解法中,你认为解法 最简捷.然后请解答下列问题,计算:![]() .
.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某汽车销售公司经销某品牌A、B两款汽车,已知A款汽车每辆进价为![]() 万元,B款汽车每辆进价为6万元.
万元,B款汽车每辆进价为6万元.
![]() 公司预计用不多于135万元且不少于129万元的资金购进这两款汽车共20辆,有几种进货方案,它们分别是什么?
公司预计用不多于135万元且不少于129万元的资金购进这两款汽车共20辆,有几种进货方案,它们分别是什么?
![]() 如果A款汽车每辆售价为9万元,B款汽车每辆售价为8万元,为打开B款汽车的销路,公司决定每售出一辆B款汽车,返还顾客现金a万元,要使
如果A款汽车每辆售价为9万元,B款汽车每辆售价为8万元,为打开B款汽车的销路,公司决定每售出一辆B款汽车,返还顾客现金a万元,要使![]() 中所有的方案获利相同,a值应是多少,此种方案是什么?(提示:可设购进B款汽车x辆)
中所有的方案获利相同,a值应是多少,此种方案是什么?(提示:可设购进B款汽车x辆)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系中,二次函数y=ax2+bx+2的图象与x轴交于A(﹣3,0),B(1,0)两点,与y轴交于点C.
(1)求这个二次函数的关系解析式;
(2)点P是直线AC上方的抛物线上一动点,是否存在点P,使△ACP的面积最大?若存在,求出点P的坐标;若不存在,说明理由; 
(3)在平面直角坐标系中,是否存在点Q,使△BCQ是以BC为腰的等腰直角三角形?若存在,直接写出点Q的坐标;若不存在,说明理由;
(4)点Q是直线AC上方的抛物线上一动点,过点Q作QE垂直于x轴,垂足为E.是否存在点Q,使以点B、Q、E为顶点的三角形与△AOC相似?若存在,直接写出点Q的坐标;若不存在,说明理由;
(5)点M为抛物线上一动点,在x轴上是否存在点Q,使以A、C、M、Q为顶点的四边形是平行四边形?若存在,直接写出点Q的坐标;若不存在,说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知直线l∥AB,l与AB之间的距离为2.C、D是直线l上两个动点(点C在D点的左侧),且AB=CD=5.连接AC、BC、BD,将△ABC沿BC折叠得到△A′BC.下列说法:①四边形ABCD的面积始终为10;②当A′与D重合时,四边形ABDC是菱形;③当A′与D不重合时,连接A′、D,则∠CA′D+∠BCA′=180°;④若以A′、C、B、D为顶点的四边形为矩形,则此矩形相邻两边之和为3![]() 或7.其中正确的是( )
或7.其中正确的是( )

A. ①②④ B. ①③④ C. ①②③ D. ①②③④
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】蜗牛从某点![]() 开始沿一东西方向直线爬行,规定向东爬行的路程记为正数,向西爬行的路程记为负数.爬过的各段路程依次为(单位:厘米):
开始沿一东西方向直线爬行,规定向东爬行的路程记为正数,向西爬行的路程记为负数.爬过的各段路程依次为(单位:厘米):![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() .
.
![]() 通过计算说明蜗牛是否回到起点
通过计算说明蜗牛是否回到起点![]() .
.
![]() 蜗牛离开出发点
蜗牛离开出发点![]() 最远时是多少厘米?
最远时是多少厘米?
![]() 在爬行过程中,如果每爬
在爬行过程中,如果每爬![]() 厘米奖励
厘米奖励![]() 粒芝麻,则蜗牛一共得到多少粒芝麻?
粒芝麻,则蜗牛一共得到多少粒芝麻?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】甲、乙两工程队同时修筑水渠,且两队所修水渠总长度相等.如图是两队所修水渠长度y(米)与修筑时间x(时)的函数图象的一部分.请根据图中信息,解答下列问题: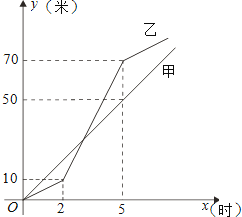
(1)①直接写出甲队在0≤x≤5的时间段内,y与x之间的函数关系式;
②直接写出乙队在2≤x≤5的时间段内,y与x之间的函数关系式;
(2)求开修几小时后,乙队修筑的水渠长度开始超过甲队?
(3)如果甲队施工速度不变,乙队在修筑5小时后,施工速度因故减少到5米/时,结果两队同时完成任务,求乙队从开修到完工所修水渠的长度为多少米?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com