
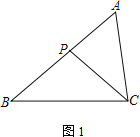
【题目】在△ABC中,P为边AB上一点.
(1) 如图1,若∠ACP=∠B,求证:AC2=AP·AB;
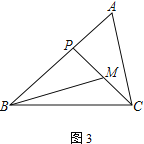
(2) 若M为CP的中点,AC=2,
① 如图2,若∠PBM=∠ACP,AB=3,求BP的长;
② 如图3,若∠ABC=45°,∠A=∠BMP=60°,直接写出BP的长.

【答案】(1)详见解析;(2)①BP=![]() ;②
;②![]() .
.
【解析】
试题分析:(1)根据已知条件易证△ACP∽△ABC,由相似三角形的性质即可证得结论;(2)①如图,作CQ∥BM交AB延长线于Q,设BP=x,则PQ=2x,易证△APC∽△ACQ,所以AC2=AP·AQ,由此列方程,解方程即可求得BP的长;②如图:作CQ⊥AB于点Q,作CP0=CP交AB于点P0,再证△AP0C∽△MPB,(2)的方法求得AP0的长,即可得BP的长.
试题解析:(1)证明:∵∠ACP=∠B,∠BAC=∠CAP,
∴△ACP∽△ABC,
∴AC:AB=AP:AC,
∴AC2=AP·AB;
(2)①如图,作CQ∥BM交AB延长线于Q,设BP=x,则PQ=2x
∵∠PBM=∠ACP,∠PAC=∠CAQ,
∴△APC∽△ACQ,
由AC2=AP·AQ得:22=(3-x)(3+x),∴x=![]()
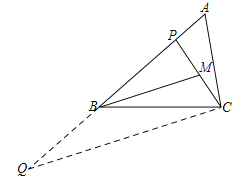
即BP=![]() ;
;
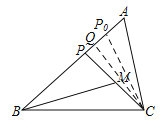
②如图:作CQ⊥AB于点Q,作CP0=CP交AB于点P0,
∵AC=2,∴AQ=1,CQ=BQ=![]() ,
,
设AP0=x,P0Q=PQ=1-x,BP=![]() -1+x,
-1+x,
∵∠BPM=∠CP0A,∠BMP=∠CAP0,
∴△AP0C∽△MPB,∴![]() ,
,
∴MP P0C=![]() AP0 BP=x(
AP0 BP=x(![]() -1+x),
-1+x),
解得x=![]()
∴BP=![]() -1+
-1+![]() =
=![]() .
.


科目:初中数学 来源: 题型:
【题目】如图,在四边形ABCD中,AD∥BC,∠ABC=90°,E是AB上一点,且DE⊥CE.若AD=1,BC=2,CD=3,则CE与DE的数量关系正确的是( )
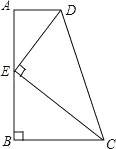
A.CE=![]() DE B.CE=
DE B.CE=![]() DE C.CE=3DE D.CE=2DE
DE C.CE=3DE D.CE=2DE
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,某沿海开放城市![]() 接到台风警报,在该市正南方向
接到台风警报,在该市正南方向![]() 的
的![]() 处有一台风中心,沿
处有一台风中心,沿![]() 方向以
方向以![]() 的速度向
的速度向![]() 移动,已知城市
移动,已知城市![]() 到
到![]() 的距离
的距离![]() .
.
(1)求台风中心经过多长时间从![]() 点移到
点移到![]() 点?
点?
(2)如果在距台风中心![]() 的圆形区域内都将有受到台风的破坏的危险,
的圆形区域内都将有受到台风的破坏的危险,
正在![]() 点休闲的游人在接到台风警报后的几小时内撤离才可脱离危险?
点休闲的游人在接到台风警报后的几小时内撤离才可脱离危险?
查看答案和解析>>
科目:初中数学 来源: 题型:
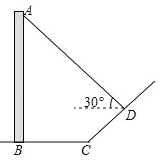
【题目】(2016山东潍坊第22题)如图,直立于地面上的电线杆AB,在阳光下落在水平地面和坡面上的影子分别是BC、CD,测得BC=6米,CD=4米,∠BCD=150°,在D处测得电线杆顶端A的仰角为30°,试求电线杆的高度(结果保留根号)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com