
【题目】如图,在正方形![]() 中,点
中,点![]() 、
、![]() 是
是![]() 边上的两点,且
边上的两点,且![]() ,过
,过![]() 作
作![]() 于
于![]() ,分别交
,分别交![]() 、
、![]() 于
于![]() ,
,![]() ,
,![]() 、
、![]() 的延长线相交于
的延长线相交于![]() .
.

(1)求证:![]() ;
;
(2)判断![]() 的形状,请说明理由.
的形状,请说明理由.
【答案】(1)见解析;(2)△PQR为等腰三角形,证明过程见解析.
【解析】
(1)可以证明△ADP≌△DCG,即可求证DP=CG.
(2)由(1)的结论可以证明△CEQ≌△CEG,进而证明∠PQR=∠QPR.故△PQR为等腰三角形.
(1)证明:在正方形ABCD中,
AD=CD,∠ADP=∠DCG=90°,
∠CDG+∠ADH=90°,
∵DH⊥AP,∴∠DAH+∠ADH=90°,
∴∠CDG=∠DAH,
∴△ADP≌△DCG,
∴DP=CG.
(2)△PQR为等腰三角形.
证明:∵CQ=DP,
∴CQ=CG,
∵四边形ABCD为正方形,
∴∠QCE=∠GCE,
又∵CE=CE,
∴△CEQ≌△CEG,
∴∠CQE=∠CGE,
∴∠PQR=∠CGE,
∵∠QPR=∠DPA,且(1)中证明△ADP≌△DCG,
∴∠PQR=∠QPR,
所以△PQR为等腰三角形.


科目:初中数学 来源: 题型:
【题目】生活中,有人喜欢把传送的便条折成“ ”形状,折叠过程按图
”形状,折叠过程按图![]() 的顺序进行(其中阴影部分表示纸条的反面):
的顺序进行(其中阴影部分表示纸条的反面):

如果由信纸折成的长方形纸条(图①)长![]() 厘米,分别回答下列问题:
厘米,分别回答下列问题:
(1)如图①、图②,如果长方形纸条的宽为![]() 厘米,并且开始折叠时
厘米,并且开始折叠时![]() 厘米,那么在图②中,
厘米,那么在图②中,![]() ____厘米.
____厘米.
(2)如图②,如果长方形纸条的宽为![]() 厘米,现在不但要折成图②的形状,还希望纸条两端超出点
厘米,现在不但要折成图②的形状,还希望纸条两端超出点![]() 的部分
的部分![]() 和
和![]() 相等,使图②. 是轴对称图形,
相等,使图②. 是轴对称图形,![]() ______厘米.
______厘米.
(3)如图④,如果长方形纸条的宽为![]() 厘米,希望纸条两端超出点
厘米,希望纸条两端超出点![]() 的部分
的部分![]() 和
和![]() 相等,即最终图形是轴对称图形,试求在开始折叠时起点
相等,即最终图形是轴对称图形,试求在开始折叠时起点![]() 与点
与点![]() 的距离(结果用
的距离(结果用![]() 表示) .
表示) .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,等边三角形![]() 的周长为
的周长为![]() ,
,![]() ,
,![]() 两点分别从
两点分别从![]() ,
,![]() 两点同时出发,点
两点同时出发,点![]() 以
以![]() 的速度按顺时针方向在三角形的边上运动,点
的速度按顺时针方向在三角形的边上运动,点![]() 以
以![]() 的速度按逆时针方向在三角形的边上运动.设
的速度按逆时针方向在三角形的边上运动.设![]() ,
,![]() 两点第一次在三角形
两点第一次在三角形![]() 的顶点处相遇的时间为
的顶点处相遇的时间为![]() ,第二次在三角形
,第二次在三角形![]() 顶点处相遇的时间为
顶点处相遇的时间为![]() ,则
,则![]() _______.
_______.
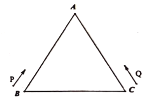
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】有A、B两组卡片共5张,A组的三张分别写有数字2,4,6,B组的两张分别写有3,5.它们除了数字外没有任何区别,
(1)随机从A组抽取一张,求抽到数字为2的概率;
(2)随机地分别从A组、B组各抽取一张,请你用列表或画树状图的方法表示所有等可能的结果.现制定这样一个游戏规则:若选出的两数之积为3的倍数,则甲获胜;否则乙获胜.请问这样的游戏规则对甲乙双方公平吗?为什么?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】观察下面的几个式子:
![]() ;
;
![]() ;
;
![]() ;
;
![]() ;…
;…
(1)根据上面的规律,第5个式子为:________________.
(2)根据上面的规律,第n个式子为:________________.
(3)利用你发现的规律,写出![]() …
…![]() ________________.
________________.
(4)利用你发现的规律,求出![]() …
…![]() 的值,并写出过程。
的值,并写出过程。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,四边形ABCD中,AB=CD,对角线AC,BD相交于点O,AE⊥BD于点E,CF⊥BD于点F,连接AF,CE,若DE=BF,则下列结论:①CF=AE;②OE=OF;③四边形ABCD是平行四边形;④图中共有四对全等三角形.其中正确结论的个数是

A.4 B.3 C.2 D.1
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】“分组合作学习”已成为推动课堂教学改革,打造自主高效课堂的重要措施.某中学从全校学生中随机抽取部分学生对“分组合作学习”实施后的学习兴趣情况进行调查分析,统计图如下:

请结合图中信息解答下列问题:
(1)求出随机抽取调查的学生人数;
(2)补全分组后学生学习兴趣的条形统计图;
(3)分组后学生学习兴趣为“中”的所占的百分比和对应扇形的圆心角.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,甲、乙两动点分别从正方形![]() 的顶点
的顶点![]() 同时沿正方形的边开始移动,甲按顺时针方向环行,乙按逆时针方向环行,若乙的速度是甲的3倍,那么它们第1次相遇在边
同时沿正方形的边开始移动,甲按顺时针方向环行,乙按逆时针方向环行,若乙的速度是甲的3倍,那么它们第1次相遇在边![]() 上.
上.

(1)它们第2次相遇在边__________上;
(2)它们第2019次相遇在边__________上.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com