
 如图,正方形ABCD的对角线相交于点O,∠CAB的平分线分别交BD、BC于E、F,作BH⊥AF于点H,分别交AC、CD于点G、P,连结GE、GF.
如图,正方形ABCD的对角线相交于点O,∠CAB的平分线分别交BD、BC于E、F,作BH⊥AF于点H,分别交AC、CD于点G、P,连结GE、GF.分析 (1)先证明△AHG≌△AHB,得出GH=BH,由线段垂直平分线的性质得出EG=EB,FG=FB;再证出∠BEF=∠BFE,得出EB=FB,因此EG=EB=FB=FG,即可得出结论;
(2)设OA=OB=OC=a,菱形BEGF的边长为b,由该菱形的性质CG=GF=b,(也可由△OAE≌△OBG得OG=OE=a-b,OC-CG=a-b,得CG=b);然后在Rt△GOE中,由勾股定理可得a和b的关系,通过相似三角形△CGP∽△AGB的对应边成比例得到:$\frac{PG}{GB}$=$\frac{CG}{AG}$;最后由(1)△OAE≌△OBG得到:AE=GB,进而得到答案.
解答 解(1)四边形BEGF是菱形,理由如下:
∵∠GAH=∠BAH,AH=AH,∠AHG=∠AHB=90°,
∴△AHG≌△AHB,
∴GH=BH,
∴AF是线段BG的垂直平分线,
∴EG=EB,FG=FB,
∵∠BEF=∠BAF+∠ABE=67.5°,∠BFE=90°-∠BAF=67.5°
∴∠BEF=∠BFE,
∴EB=FB,
∴EG=EB=FB=FG,
∴四边形BEGF是菱形.
(2)设OA=OB=OC=a,菱形BEGF的边长为b.
∵四边形BEGF是菱形,
∴GF∥OB,
∴∠CGF=∠COB=90°,
∴∠GFC=∠GCF=45°,
∴CG=GF=b,
∵四边形ABCD是正方形,
∴OA=OB,∠AOE=∠BOG=90°
∵BH⊥AF,
∴∠GAH+∠AGH=90°=∠OBG+∠AGH.
∴∠GAH=∠OBG,
∴△OAE≌△OBG.
∴OG=OE=a-b.
∵在Rt△GOE中,GE=$\sqrt{2}$OG,
∴b=$\sqrt{2}$(a-b),整理得a=$\frac{2+\sqrt{2}}{2}$b.
∴AC=2a=(2+$\sqrt{2}$)b,AG=AC-CG=(1+$\sqrt{2}$)b.
∵PC∥AB,
∴$\frac{BG}{PG}$=$\frac{AG}{CG}$=$\frac{(1+\sqrt{2})b}{b}$=1+$\sqrt{2}$,
由△OAE≌△OBG得AE=BG,
∴$\frac{AE}{PG}$=1+$\sqrt{2}$.
点评 本题考查了正方形的性质、全等三角形的判定与性质、线段垂直平分线的性质、菱形的判定;熟练掌握正方形的性质,并能进行推理论证是解决问题的关键.


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:解答题
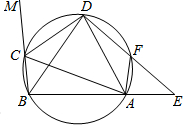 如图,在圆内接四边形ABCD中,CD为∠BAC的外角平分线,F为$\widehat{AD}$上一点,BC=AF,延长DF与BA的延长线交于E.
如图,在圆内接四边形ABCD中,CD为∠BAC的外角平分线,F为$\widehat{AD}$上一点,BC=AF,延长DF与BA的延长线交于E.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
 如图,△ABC中,∠ACB=90°,sinB=$\frac{\sqrt{3}}{2}$,BC=1,点D为斜边AB的中点,过A、C、D三点作⊙O,点P为AC所对的优弧上任意一点,点M、N分别为线段AC、AP的中点,则MN的最大值为1.
如图,△ABC中,∠ACB=90°,sinB=$\frac{\sqrt{3}}{2}$,BC=1,点D为斜边AB的中点,过A、C、D三点作⊙O,点P为AC所对的优弧上任意一点,点M、N分别为线段AC、AP的中点,则MN的最大值为1.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
| 服装价格 | 甲 | 乙 |
| 进价(元/件) | m | m-30 |
| 售价(元/件) | 320 | 280 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,在等边△ABC中,D是BC边的中点,以AD为边作等边△ADE.取AB边的中点F,连接CF、CE,试判断四边形AFCE的形状.并说明理由.
如图,在等边△ABC中,D是BC边的中点,以AD为边作等边△ADE.取AB边的中点F,连接CF、CE,试判断四边形AFCE的形状.并说明理由.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com