
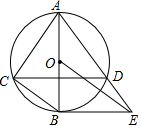
 如图,AB是⊙O的直径,过点B作⊙O的切线BE,AE交⊙O于点D,弦DC∥BE,且DA=DC,若DE=2,则OE的长为$\frac{8\sqrt{3}}{3}$.
如图,AB是⊙O的直径,过点B作⊙O的切线BE,AE交⊙O于点D,弦DC∥BE,且DA=DC,若DE=2,则OE的长为$\frac{8\sqrt{3}}{3}$. 分析 根据题意作出合适的辅助线,然后根据在直角三角形中,30°角所对的直角边是斜边的一半和锐角三角函数可以解答本题.
解答 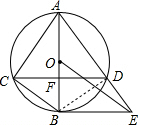 解:如右图所示,连接BD,
解:如右图所示,连接BD,
∵DA=DC,BE是⊙O的切线,弦DC∥BE,
∴∠ABE=90°,∠AFD=∠ABE=90°,
∴AF⊥CD,AF平分CD,
∴CF=DF,
∴AD=2DF,
∴∠DAF=30°,
∵∠ADB=90°,∠ABE=90°,
∴∠ABD=60°,∠DBE=30°,
∵DE=2,
∴BE=4,
∵cos∠OEB=$\frac{BE}{OE}$,∠OEB=30°,
∴OE=$\frac{8\sqrt{3}}{3}$,
故答案为:$\frac{8\sqrt{3}}{3}$.
点评 本题考查切线的性质,解题的关键是明确题意,找出所求问题需要的条件.


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:解答题
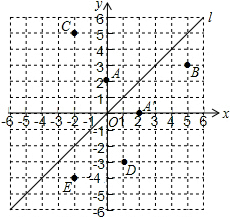 如图,在平面直角坐标系xOy中,直线l是第一、三象限的角平分线.
如图,在平面直角坐标系xOy中,直线l是第一、三象限的角平分线.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 7<b≤8 | B. | 2<b≤3 | C. | 8≤b<9 | D. | 7≤b<8 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
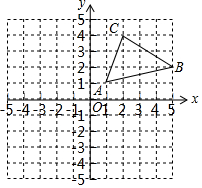 已知如图,△ABC的顶点均在格点上,点C的坐标是(2,4).
已知如图,△ABC的顶点均在格点上,点C的坐标是(2,4).查看答案和解析>>
科目:初中数学 来源: 题型:选择题
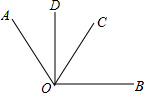 如图,OC是∠AOB的平分线,∠AOD:∠BOD=1:3,若∠COD=25°,则∠AOB的度数为( )
如图,OC是∠AOB的平分线,∠AOD:∠BOD=1:3,若∠COD=25°,则∠AOB的度数为( )| A. | 100° | B. | 80° | C. | 70° | D. | 60° |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com