
分析 分别过点M、N作x轴垂线与直线交点即为所求,由M、N点坐标可得点A坐标;在直线上取一点(x,-x+1),根据AM2+AN2=MN2列出关于x的方程,解方程可得第三种情况下点A的坐标.
解答 解:①如图,过点M(-3,0)作x轴垂线交直线y=-x+1于点A1,则A1的坐标为(-3,4);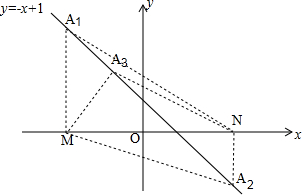
②过点N(3,0)作x轴垂线交直线y=-x+1于点A2,则A2的坐标为(3,-2);
③设直线y=-x+1上的点A3坐标为(x,-x+1),
根据题意,A3M2+A3N2=MN2,即(-3-x)2+(x-1)2+(3-x)2+(x-1)2=62,
整理,得:x2-4x-4=0,
解得:x=$\frac{1±\sqrt{17}}{2}$,
当x=$\frac{1+\sqrt{17}}{2}$时,y=-$\frac{1+\sqrt{17}}{2}$+1=$\frac{1-\sqrt{17}}{2}$,
当x=$\frac{1-\sqrt{17}}{2}$时,y=-$\frac{1-\sqrt{17}}{2}$+1=$\frac{1+\sqrt{17}}{2}$,
∴点A3的坐标为($\frac{1+\sqrt{17}}{2}$,$\frac{1-\sqrt{17}}{2}$)或($\frac{1-\sqrt{17}}{2}$,$\frac{1+\sqrt{17}}{2}$),
故答案为:(-3,4)、(3,-2)、($\frac{1+\sqrt{17}}{2}$,$\frac{1-\sqrt{17}}{2}$)或($\frac{1-\sqrt{17}}{2}$,$\frac{1+\sqrt{17}}{2}$).
点评 本题主要考查一次函数图象上点的坐标、两点间距离公式、勾股定理,根据勾股定理列出关于x的方程是解题的关键.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:填空题
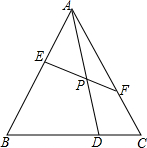 如图,等边△ABC中,D是BC边上一点,BD=2DC,P是线段AD上的动点,过点P的直线交边AB、AC于点E、F,且∠APE=60°,则PE:PF=4:3.
如图,等边△ABC中,D是BC边上一点,BD=2DC,P是线段AD上的动点,过点P的直线交边AB、AC于点E、F,且∠APE=60°,则PE:PF=4:3.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,在△ABC中.∠B=60°,⊙0是△ABC的外接圆.过点A的直线交CO的延长线于点P,CP交⊙O于点D,且满足PA2=PD•PC.
如图,在△ABC中.∠B=60°,⊙0是△ABC的外接圆.过点A的直线交CO的延长线于点P,CP交⊙O于点D,且满足PA2=PD•PC.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com