练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情
    12．观察下列各式，并回答问题
    1=12
    1+3=4=22
    1+3+5=9=32
    1+3+5+7=16=42
    …
    （1）请你写出第10个式子；
    （2）计算：1+3+5+7+…+2013；
    （3）计算：1005+1007+…+2013．

    分析 （1）由1+3=4=22，1+3+5=9=32，1+3+5+7=16=42，1+3+5+7+9=25=52，…可以看出连续奇数的和等于数的个数的平方；由此可以写出第10个式子；
    （2）根据（1）中的规律可直接计算出结果；
    （3）1005+1007+…+2013=（1+3+5+…+2013）-（1+3+5+…+1003），再用（1）中的规律计算即可．

    解答 解：第n个式子1+3+5+7+9+…+2n-1=n2；
    （1）第10个式子1+3+5+7+9+11+13+15+17+19+21=121=112；

    （2）1+3+5+7+9…+1003+1005+…+2013=10072；

    （4）原式=（1+3+5+…+2013）-（1+3+5+…+1003）
    =10072-5022
    =762045．

    点评 此题主要考查了数字的变化规律，探寻数列规律，连得出连续奇数的和等于数的个数的平方是解决问题的关键．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：填空题

    2．若抛物线y=-x2+2（a-2）x-2的顶点在y轴的左侧，求a的取值范围a＜2．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    3．如图，在?ABCD中，E为AB的中点，点F在AD上，EF交AC于点G，AF=2，DF=4，AG=3，求AC的长．

    查看答案和解析>>

    科目：初中数学 来源： 题型：填空题

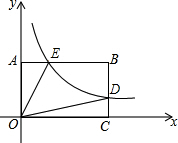    20．如图，反比例函数y=$\frac{k}{x}$（k＞0）图象过矩形OABC边BC中点D交AB于点E，四边形ODBE的面积为2，则结论：①S△OAE=S△OCD；②E为AB中点；③k=2；④AO=AE，其中正确的序号为①②③．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    7．已知a：b=c：d，且b≠nd，求证：$\frac{a}{b}$=$\frac{a-nc}{b-nd}$．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    17．两个多项式x+ax-1与x2+5x-6的乘积中不含x3项，试求a的值．

    查看答案和解析>>

    科目：初中数学 来源： 题型：填空题

    4．已知反比例函数y=$\frac{2k}{x}$，当x＜0时，y随x增大而减小，与直线y=-x+$\sqrt{3}k$都过点P，且OP=$\sqrt{7}$，则k的值为$\frac{7}{3}$．

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

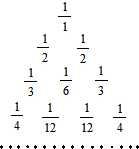    1．如图所示的数阵叫“莱布尼兹调和三角形”，它们是由整数的倒数组成的，第n行有n个数，且两端的数均为$\frac{1}{n}$，每个数是它下一行左右相邻两数的和，则第8行第2个数（从左到右）为（　　）
    A．$\frac{1}{56}$B．$\frac{1}{60}$C．$\frac{1}{64}$D．$\frac{1}{168}$

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    2．若|a-2|+（3+b）2=0，则a、b的值是多少？

    查看答案和解析>>

    同步练习册答案