
【题目】如图①,抛物线y=﹣![]() x2+x+4与x轴交于A,B两点,与y轴交于点C,点D为线段AC的中点,直线BD与抛物线交于另一点E,与y轴交于点F.
x2+x+4与x轴交于A,B两点,与y轴交于点C,点D为线段AC的中点,直线BD与抛物线交于另一点E,与y轴交于点F.
(1)求直线BD的解析式;
(2)如图②,点P是直线BE上方抛物线上一动点,连接PD,PF,当△PDF的面积最大时,在线段BE上找一点G,使得PG﹣![]() GE的值最小,求出点G的坐标及PG﹣
GE的值最小,求出点G的坐标及PG﹣![]() GE的最小值;
GE的最小值;
(3)将抛物线沿直线AC平移,点A,C平移后的对应点为A′,C'.在平面内有一动点H,当以点B,A',C',H为顶点的四边形为平行四边形时,在直线AC上方找一个满足条件的点H,与直线AC下方所有满足条件的点H为顶点的多边形为轴对称图形时,求出点A′的坐标.

【答案】(1)y=![]() x+1;(2)点G(
x+1;(2)点G(![]() ,
,![]() ),最小值为
),最小值为![]() ;(3)(3,1)、(
;(3)(3,1)、(![]() +1,3﹣
+1,3﹣![]() )、(1﹣
)、(1﹣![]() ,3+
,3+![]() )、(5+
)、(5+![]() ,﹣
,﹣![]() ﹣1)、(5﹣
﹣1)、(5﹣![]() ,
,![]() ﹣1).
﹣1).
【解析】
(1)令-![]() x2+x+4=0,可求出点A和点B的坐标,令x=0,可求出点C的坐标,再根据点D时AC的中点,可求出点D的坐标,利用待定系数法求直线解析式即可.(2)求三角形的面积最值可以转化为求线段长度的最大值,利用点坐标表示线段长度,配方求最值,求PG-
x2+x+4=0,可求出点A和点B的坐标,令x=0,可求出点C的坐标,再根据点D时AC的中点,可求出点D的坐标,利用待定系数法求直线解析式即可.(2)求三角形的面积最值可以转化为求线段长度的最大值,利用点坐标表示线段长度,配方求最值,求PG-![]() GE的最小值,可将不共线的线段转换为共线的线段长度.(3)理解题意利用轴对称图形就是找等腰三角形,再分情况讨论即可.
GE的最小值,可将不共线的线段转换为共线的线段长度.(3)理解题意利用轴对称图形就是找等腰三角形,再分情况讨论即可.
解:(1)令﹣![]() x2+x+4=0,解得x1=﹣2,x2=4,
x2+x+4=0,解得x1=﹣2,x2=4,
∴B(﹣2,0),A(4,0),
令x=0,y=4,
∴C(0,4),
∵D为AC的中点,
∴D(2,2),
设直线BD的解析式为y=kx+b(k≠0),代入点B和点D,
![]() ,
,
解得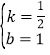 ,
,
∴直线BD的解析式为y=![]() x+1.
x+1.
(2)如图所示
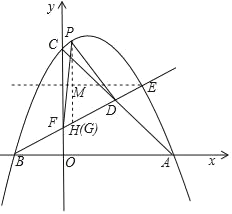
过点P作y轴的平行线,交BE交于点H,
设点P的坐标为(t,﹣![]() t2+t+4),
t2+t+4),
则点H为(t,![]() t+1),
t+1),
∴PH=﹣![]() t2+t+4﹣(
t2+t+4﹣(![]() t+1)=﹣
t+1)=﹣![]() (t﹣
(t﹣![]() )2+
)2+![]() ,
,
当t=![]() 时,PH最大,此时点P为(
时,PH最大,此时点P为(![]() ,
,![]() ),
),
当PH最大时,△PDF的面积也最大.
∵直线BD的解析式为y=![]() x+1,
x+1,
令x=0,y=1,∴点F(0,1),
在Rt△BFO中,根据勾股定理,BF=![]() ,
,
∴sin∠FBO=![]()
过点E作x轴的平行线与过点G作y轴的平行线交于点M,
∴∠MEG=∠FBO,
∴MG=EGsin∠MEG=![]() EG,
EG,
∴PG﹣![]() GE=PG﹣MG,
GE=PG﹣MG,
当P、M、G三点共线时,PG﹣MG=PM,否则都大于PM,
∴当P、M、G三点共线时,PG﹣MG最小,此时点G与点H重合,
令﹣![]() x2+x+4=
x2+x+4=![]() x+1,
x+1,
解得x1=3,x2=﹣2,
∴点E(3,![]() ),
),
∴PM=![]() ﹣
﹣![]() =
=![]() ,
,
∴点G(![]() ,
,![]() ),
),
∴点G(![]() ,
,![]() ),PG﹣
),PG﹣![]() GE的最小值为
GE的最小值为![]() .
.
(3)如图所示,

当以点B,A',C',H为顶点的四边形为平行四边形时,
在直线AC下方的点H只有两个,点H1和点H2,
过点B作AC的平行线交y轴于点G,∴G(0,﹣2)
∵点A(4,0),点C(0,4),
∴AC=4![]() ,
,
∴BH1=BH2=4![]() ,
,
∵∠CAO=45°,
∴H1(﹣6,4),H2(2,﹣4),
在y轴上截取点E,使EC=CG,则点E(0,10),
过点E作AC的平行线,则在直线AC上方的点H一定在这条平行线上,
当△H1H2H3为等腰三角形时即为轴对称图形,
①当H1H3=H2H3时,
直线EH3的解析式为y=﹣x+10,
设H3(m,﹣m+10),
H1H3=![]() ,
,
H2H3=![]() ,
,
解得m=4,∴H3(4,6),
∴A′(3,1).
②当H1H3=H1H2时,
∵H1H3=![]() ,H1H2=8
,H1H2=8![]() ,
,
解得m1=2![]() ,m2=﹣2
,m2=﹣2![]() ,此时点H3(2
,此时点H3(2![]() ,10﹣2
,10﹣2![]() )或(﹣2
)或(﹣2![]() ,10+2
,10+2![]() ),
),
∴A′(![]() +1,3﹣
+1,3﹣![]() )或(1﹣
)或(1﹣![]() ,3+
,3+![]() ).
).
③当H2H3=H1H2时,
∵H2H3=![]() ,H1H2=8
,H1H2=8![]() ,
,
解得m1=8+2![]() ,m2=8﹣2
,m2=8﹣2![]() ,此时点H3(8+2
,此时点H3(8+2![]() ,2﹣2
,2﹣2![]() )或(8﹣2
)或(8﹣2![]() ,2+2
,2+2![]() ),
),
∴A′(5+![]() ,﹣
,﹣![]() ﹣1)或(5﹣
﹣1)或(5﹣![]() ,
,![]() ﹣1).
﹣1).
综上所述,点A′的坐标为(3,1)、(![]() +1,3﹣
+1,3﹣![]() )、(1﹣
)、(1﹣![]() ,3+
,3+![]() )、(5+
)、(5+![]() ,﹣
,﹣![]() ﹣1)、(5﹣
﹣1)、(5﹣![]() ,
,![]() ﹣1).
﹣1).


科目:初中数学 来源: 题型:
【题目】如图,正方形ABCD中,M为BC上一点,F是AM的中点,EF⊥AM,垂足为F,交AD的延长线于点E,交DC于点N.

(1)求证:△ABM∽△EFA;
(2)若AB=12,BM=5,求DE的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,反比例函数![]() 的图象与正比例函数
的图象与正比例函数![]() 图象交于点
图象交于点![]() ,且点
,且点![]() 的横坐标为2.
的横坐标为2.
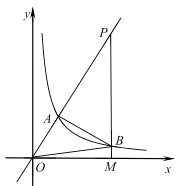
(1)求反比例函数的表达式;
(2)若射线![]() 上有一点
上有一点![]() ,且
,且![]() ,过点
,过点![]() 作
作![]() 与
与![]() 轴垂直,垂足为
轴垂直,垂足为![]() ,交反比例函数图象于点
,交反比例函数图象于点![]() ,连接
,连接![]() ,
,![]() ,请求出
,请求出![]() 的面积.
的面积.
(3)定义:横纵坐标均为整数的点称为“整点”.在(2)的条件下,请探究边![]() ,
,![]() 与反比例函数图象围成的区域内(不包括边界)“整点”的个数.
与反比例函数图象围成的区域内(不包括边界)“整点”的个数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某建设工地一个工程有大量的沙石需要运输.建设公司车队有载重量为8吨和10吨的卡车共12辆,全部车辆一次能运输110吨沙石
(1)求建设公司车队载重量为8吨和10吨的卡车各有多少辆?
(2)随着工程的进展,车队需要一次运输沙石超过160吨,为了完成任务,准备新增购这两种卡车共6辆,车队最多新购买载重量为8吨的卡车多少辆?
查看答案和解析>>
科目:初中数学 来源: 题型:
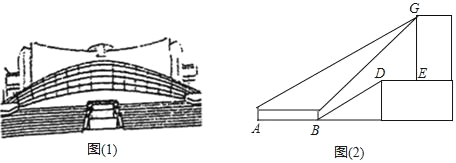
【题目】如图(1)是重庆中国三峡博物馆,又名重庆博物馆,中央地方共建国家级博物馆图(2)是侧面示意图.某校数学兴趣小组的同学要测量三峡博物馆的高GE.如(2),小杰身高为1.6米,小杰在A处测得博物馆楼顶G点的仰角为27°,前进12米到达B处测得博物馆楼顶G点的仰角为39°,斜坡BD的坡i=1:2.4,BD长度是13米,GE⊥DE,A、B、D、E、G在同一平面内,则博物馆高度GE约为_____米.(结果精确到1米,参考数据tan27°≈0.50,tan39°≈0.80)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某商场试销一种成本为![]() 元/件的T 恤,规定试销期间单价不低于成本单价,又获利不得高于
元/件的T 恤,规定试销期间单价不低于成本单价,又获利不得高于![]() ,经试销发现,销售量
,经试销发现,销售量![]() (件)与销售单价
(件)与销售单价![]() (元/件)符合一次函数
(元/件)符合一次函数![]() ,且
,且![]() 时,
时,![]() ;
;![]() 时,
时,![]() .
.
(1)写出销售单价![]() 的取值范围;
的取值范围;
(2)求出一次函数![]() 的解析式;
的解析式;
(3)若该商场获得利润为![]() 元,试写出利润
元,试写出利润![]() 与销售单价
与销售单价![]() 之间的关系式,销售单价定为多少时,商场可获得最大利润,最大利润是多少?
之间的关系式,销售单价定为多少时,商场可获得最大利润,最大利润是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某中学为了了解学生平均每天“诵读经典”的时间,在全校范围内随机抽查了部分学生进行调查统计,并将调查统计的结果分为四类,每天诵读时间t≤20分钟的学生记为A类,20分钟<t≤40分钟的学生记为B类,40分钟<t≤60分钟的学生记为C类,t>60分钟的学生记为D类.将收集的数据绘制成如下两幅不完整的统计图.请根据图中提供的信息,解答下列问题:

(1)这次共抽查了 名学生进行调查统计,m= ,n= ;
(2)请补全上面的条形图;
(3)如果该校共有1600名学生,请你估计该校C类学生约有多少人.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】点G为△ABC的重心(△ABC三条中线的交点),以点G为圆心作⊙G与边AB,AC相切,与边BC相交于点H,K,若AB=4,BC=6,则HK的长为( )
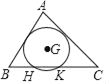
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在同一平面直角坐标系中,一次函数![]() 与反比例函数
与反比例函数![]() (
(![]() 为常数,且
为常数,且![]() )的图像交于
)的图像交于![]() 、
、![]() 两点,它们的部分图像如图所示,
两点,它们的部分图像如图所示,![]() 的面积是6.
的面积是6.
(1)求一次函数![]() 与反比例函数
与反比例函数![]() 的表达式;
的表达式;
(2)请直接写出不等式![]() 的解集.
的解集.
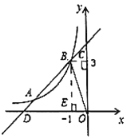
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com