
【题目】如图,AB是⊙0的直径,AB=10,CD是⊙0的切线,C为切点,交直线AB于E,AD⊥CD于D,AD=2CD.
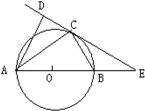
(1)求证:∠CAB=∠CAD;
(2)求CD的长;
(3)求AE的长.
【答案】(1)证明过程见解析;(2)4;(3)![]() .
.
【解析】
(1)根据切线和垂直得出∠OCA=∠DAC,再根据OA=OC得出∠OCA=∠OAC,即可得出答案;
(2)先求出△ACB∽△ADC得出AC=2CB,再结合勾股定理求出CB和AC的值,进而在△ACD中利用勾股定理求出CD和AD的值,即可得出答案;
(3)根据已知证出△ADE∽△OCE,再根据相似三角形对应边成比例即可得出答案.

(1)连接OC
∵CD是圆O的切线
∴∠OCD=∠OCE=90°
∴∠OCA+∠ACD=90°
又AD⊥CD
∴∠DAC+∠DCA=90°
∴∠OCA=∠DAC
又∵OC=OA
∴∠OCA=∠OAC
∴∠BAC=∠DAC
(2)∵AB是圆O的直径
∴∠ACB=90°
∴△ACB∽△ADC
又AD=2CD
∴AC=2CB
设AC=2x,CB=x
![]()
解得:![]() (负值舍去)
(负值舍去)
设CD=y,则AD=2y
则![]()
解得:y=±4(负值舍去)
∴CD=4
(3)∵CD=4,AD=8
∵AB是圆O的直径,AB=10
∴OA=OB=5
∴OE=AE-OA=AE-5
∵∠ADE=∠OCE,∠E=∠E
∴△ADE∽△OCE
∴![]()
即![]()
解得:AE=![]()


 走进文言文系列答案
走进文言文系列答案科目:初中数学 来源: 题型:
【题目】如图,在四边形纸片ABCD中,AD∥BC,AD>CD,将纸片沿过点D的直线折叠,使点C落在AD上的点C′处,折痕DE交BC于点E,连结C′E.
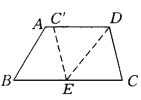
(1)求证:四边形CDC′E是菱形;
(2)若BC=CD+AD,试判断四边形ABED的形状,并加以证明.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在如图的菱形网格图中,每个小菱形的边长均为![]() 个单位,且每个小菱形内角中的锐角为60°.
个单位,且每个小菱形内角中的锐角为60°.
(1)直接写出![]() 的三个顶点
的三个顶点![]() 的坐标;
的坐标;
(2)在图中作出![]() 以点
以点![]() 为旋转中心,沿顺时针方向旋转60°后的图形
为旋转中心,沿顺时针方向旋转60°后的图形![]() ;
;
(3)根据(2),请直接写出线段![]() 扫过的面积.
扫过的面积.
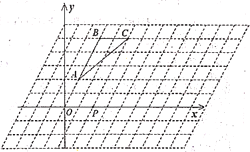
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,D是AB的中点,E是CD的中点, 过点C作CF//AB交AE的延长线于点F,连接BF.
(1) 求证:DB=CF;
(2) 如果AC=BC,试判断四边形BDCF的形状,并证明你的结论.
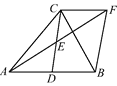
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系![]() 中,直线
中,直线![]() 与双曲线
与双曲线![]() 相交于点
相交于点![]() .
.
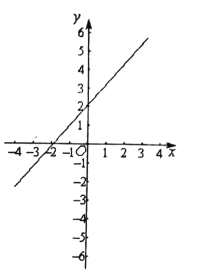
(1)求反比例函数的表达式;
(2)画出双曲线的示意图;
(3)若另一个交点![]() 的坐标为
的坐标为![]() ,则
,则![]() ;当
;当![]() 时,
时,![]() 的取值范围 .
的取值范围 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,真线![]() 与
与![]() 轴,
轴,![]() 轴分别交于
轴分别交于![]() 、
、![]() 两点,
两点,![]() 为等腰直角三角形,且
为等腰直角三角形,且![]() .若点
.若点![]() 恰好落在函数
恰好落在函数![]() (
(![]() )在第二象限内的图象上,则
)在第二象限内的图象上,则![]() 的值为( )
的值为( )
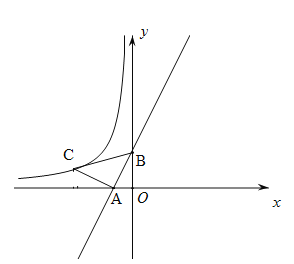
A.-1B.-2C.-3D.-4
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,阳光下,小亮的身高如图中线段AB所示,他在地面上的影子如图中线段BC所示,线段DE表示旗杆的高,线段FG表示一堵高墙.
(1)请你在图中画出旗杆在同一时刻阳光照射下形成的影子,并用线段表示;
(2)如果小亮的身高AB=1.6m,他的影子BC=2.4m,旗杆的高DE=15m,旗杆与高墙的距离EG=16m,请求出旗杆的影子落在墙上的长度.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某企业设计了一款工艺品,每件的成本是50元,为了合理定价,投放市场进行试销.据市场调查,销售单价是100元时,每天的销售量是50件,而销售单价每降低1元,每天就可多售出5件,但要求销售单价不得低于成本.
(1)当销售单价为70元时,每天的销售利润是多少?
(2)求出每天的销售利润y(元)与销售单价x(元)之间的函数关系式,并求出自变量![]() 的取值范围;
的取值范围;
(3)如果该企业每天的总成本不超过7000元,那么销售单价为多少元时,每天的销售利润最大?最大利润是多少?(每天的总成本=每件的成本×每天的销售量)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com