
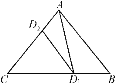
【题目】定义:若经过三角形顶点的一条直线把三角形分割出至少一个图形与原三角形相似,则称这条直线为三角形的自似线,如图,△ABC中,AC=b,BC=a,∠C<∠B<∠A,过顶点A作∠CAD1=∠B,交边BC于点D1,依次过顶点D1作∠CD1D2=∠CAD1,过点D2作∠CD2D3=∠CD1D2,…,过点Dn-1作∠CDn-1Dn=∠CDn-2Dn-1.
(1)试证直线AD1是△ABC的自似线;
(2)试求线段CD1的长,并猜想CDn的长;
(3)当60°<∠A<120°,且n=5时,与△ABC相似的三角形有几个?
【答案】(1)证明见解析;(2) CD1=![]() ,
, ![]() ;(3)当∠ A=90°时,与△ABC相似的三角形有10个;当∠ A≠90°时,与△ABC相似的三角形有5个.
;(3)当∠ A=90°时,与△ABC相似的三角形有10个;当∠ A≠90°时,与△ABC相似的三角形有5个.
【解析】
(1)由∠C=∠ C,∠CAD1=∠ B,得△CAD1∽△CBA,即直线AD1是△ABC的自似线.
(2)由(1)得△CAD1∽△CBA,![]() , 可得CD1=
, 可得CD1=![]() ,
,![]() .
.
(3)画图可知当∠ A=90°时,与△ABC相似的三角形有10个;当∠ A≠90°时,与△ABC相似的三角形有5个.
(1)证明:∵∠C=∠ C,∠CAD1=∠ B,
∴△CAD1∽△CBA,
∴直线AD1是△ABC的自似线.
(2)由(1)得△CAD1∽△CBA,
∴![]() ,
,
∴CD1=![]() ,
, ![]() .
.
(3)当∠ A=90°时,与△ABC相似的三角形有10个;当∠ A≠90°时,与△ABC相似的三角形有5个.


 开心快乐假期作业暑假作业西安出版社系列答案
开心快乐假期作业暑假作业西安出版社系列答案 名题训练系列答案
名题训练系列答案科目:初中数学 来源: 题型:
【题目】如图,抛物线![]() (a≠0)的对称轴为直线x=1,与x轴的一个交点坐标为(﹣1,0),其部分图象如图所示,下列结论:
(a≠0)的对称轴为直线x=1,与x轴的一个交点坐标为(﹣1,0),其部分图象如图所示,下列结论:
①4ac<b2;
②方程![]() 的两个根是x1=﹣1,x2=3;
的两个根是x1=﹣1,x2=3;
③3a+c>0
④当y>0时,x的取值范围是﹣1≤x<3
⑤当x<0时,y随x增大而增大
其中结论正确的个数是( )

A. 4个 B. 3个 C. 2个 D. 1个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,Rt△ACB中,∠ACB=90°,△ABC的角平分线AD、BE相交于点P,过P作PF⊥AD交BC的延长线于点F,交AC于点H,则下列结论:①∠APB=135°;②BF=BA;③PH=PD;④连接CP,CP平分∠ACB,其中正确的是( )

A. ①②③ B. ①②④ C. ①③④ D. ①②③④
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点M、N分别是正五边形ABCDE的边BC、CD上的点,且BM=CN,AM交BN于点P.
(1)求证:△ABM≌△BCN;
(2)求∠APN的度数.

查看答案和解析>>
科目:初中数学 来源: 题型:
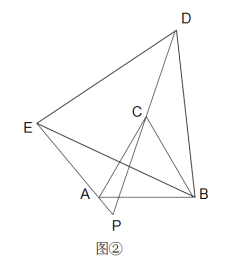
【题目】如图, AB=CB, BD=BE, ∠ABC=∠DBE=a.
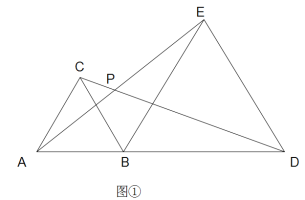
(1)当a=60°, 如图①则,∠DPE的度数______________
(2)若△BDE绕点B旋转一定角度,如图②所示,求∠DPE(用a表示)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,四边形ABCD中,∠B=90°, AB//CD,M为BC边上的一点,AM平分∠BAD,DM平分∠ADC,

求证:(1) AM⊥DM;
(2) M为BC的中点.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在北海市创建全国文明城活动中,需要30名志愿者担任“讲文明树新风”公益广告宣传工作,其中男生18人,女生12人.
(1)若从这30人中随机选取一人作为“展板挂图”讲解员,求选到女生的概率;
(2)若“广告策划”只在甲、乙两人中选一人,他们准备以游戏的方式决定由谁担任,游戏规则如下:将四张牌面数字分别为2,3,4,5的扑克牌洗匀后,数字朝下放于桌面,从中任取2张,若牌面数字之和为偶数,则甲担任,否则乙担任.试问这个游戏公平吗?请用树状图或列表法说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,![]() 轴,
轴,![]() 轴,点
轴,点![]() 在x轴上,A(1,2),B(-1,2),D(-3,0),E(-3,-2),G(3,-2)把一条长为2018个单位长度且没有弹性的细线(线的粗细忽略不计)的一端固定在点A处,并按A-B-D-E-F-G-H-P-A…的规律紧绕在图形“凸”的边上,则细线另一端所在位置的点的坐标是()
在x轴上,A(1,2),B(-1,2),D(-3,0),E(-3,-2),G(3,-2)把一条长为2018个单位长度且没有弹性的细线(线的粗细忽略不计)的一端固定在点A处,并按A-B-D-E-F-G-H-P-A…的规律紧绕在图形“凸”的边上,则细线另一端所在位置的点的坐标是()

A.(1,1)B.(1,2)
C.(1,2)D.(1,0)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,四边形OABC的顶点O是坐标原点,点A在第一象限,点C在第四象限且OC=5,点B在x轴的正半轴上且OB=6,∠OAB=90°且OA=AB.
(1)求点A和点B的坐标;
(2)点P是线段OB上的一个动点(点P不与点O,B重合),过点P的直线l与y轴平行,直线l交边OA成边AB于点Q,交边OC或边CB于点R,设点P的横坐标为t,线段QR的长度为m,已知t=4时,直线l恰好过点C,当0<t<3时,求m关于t的函数关系式.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com