
 的一元二次方程
的一元二次方程 ,
, (其中
(其中 ),若
),若 是关于m的函数,且
是关于m的函数,且 ,求这个函数的解析式。
,求这个函数的解析式。科目:初中数学 来源: 题型:
(12分)如图,已知关于![]() 的一元二次函数
的一元二次函数![]() (
(![]() )的图象与
)的图象与![]() 轴相交于
轴相交于![]() 、
、![]() 两点(点
两点(点![]() 在点
在点![]() 的左侧),与
的左侧),与![]() 轴交于点
轴交于点![]() ,且
,且![]() ,顶点为
,顶点为![]() .
.

1.⑴ 求出一元二次函数的关系式;
2.⑵点![]() 为线段
为线段![]() 上的一个动点,过点
上的一个动点,过点![]() 作
作![]() 轴的垂线
轴的垂线![]() ,垂足为
,垂足为![]() .若
.若![]() ,
,![]() 的面积为
的面积为![]() ,求
,求![]() 关于
关于![]() 的函数关系式,并写出
的函数关系式,并写出![]() 的取值范围;
的取值范围;
3.⑶ 探索线段![]() 上是否存在点
上是否存在点![]() ,使得
,使得![]() 为直角三角形,如果存在,求出
为直角三角形,如果存在,求出![]() 的坐标;如果不存在,请说明理由.
的坐标;如果不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
 (12分)如图,已知关于
(12分)如图,已知关于 的一元二次函数
的一元二次函数 (
( )的图象与
)的图象与 轴相交于
轴相交于 、
、 两点(点
两点(点 在点
在点 的左侧),与
的左侧),与 轴交于点
轴交于点 ,且
,且 ,顶点为
,顶点为 .
.
 点
点 为线段
为线段 上的一个动点,过点
上的一个动点,过点 作
作 轴的垂线
轴的垂线 ,垂足为
,垂足为 .若
.若 ,
, 的面积为
的面积为 ,求
,求 关于
关于 的函数关系式,并写出
的函数关系式,并写出 的取值范围;
的取值范围; 上是否存在点
上是否存在点 ,使得
,使得 为直角三角形,如果存在,求出
为直角三角形,如果存在,求出 的坐标;如果不存在,请说明理由.
的坐标;如果不存在,请说明理由.查看答案和解析>>
科目:初中数学 来源:2013届江苏省仪征市九年级第二次模拟考试数学试卷(带解析) 题型:解答题
如图,已知关于 的一元二次函数
的一元二次函数 (
( )的图象与
)的图象与 轴相交于
轴相交于 、
、 两点(点
两点(点 在点
在点 的左侧),与
的左侧),与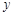 轴交于点
轴交于点 ,且
,且 ,顶点为
,顶点为 .
.
(1)求出一元二次函数的关系式;
(2)点 为线段
为线段 上的一个动点,过点
上的一个动点,过点 作
作 轴的垂线
轴的垂线 ,垂足为
,垂足为 .若
.若 ,
, 的面积为
的面积为 ,求
,求 关于
关于 的函数关系式,并写出
的函数关系式,并写出 的取值范围;
的取值范围;
(3)在(2)的条件下,当 点坐标是 时,
点坐标是 时,  为直角三角形.
为直角三角形.
查看答案和解析>>
科目:初中数学 来源:2013届江苏省泰州市永安初级中学九年级下学期第二次涂卡训练数学试卷(带解析) 题型:解答题
如图,已知关于 的一元二次函数
的一元二次函数 (
( )的图象与
)的图象与 轴相交于
轴相交于 、
、 两点(点
两点(点 在点
在点 的左侧),与
的左侧),与 轴交于点
轴交于点 ,且
,且 ,顶点为
,顶点为 .
.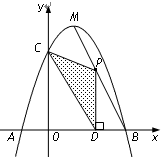
(1)求出一元二次函数的关系式;
(2)点 为线段
为线段 上的一个动点,过点
上的一个动点,过点 作
作 轴的垂线
轴的垂线 ,垂足为
,垂足为 .若
.若 ,
, 的面积为
的面积为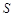 ,求
,求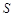 关于
关于 的函数关系式,并写出
的函数关系式,并写出 的取值范围;
的取值范围;
(3)在(2)的条件下,当 点坐标是 时,
点坐标是 时, 为直角三角形.
为直角三角形.
查看答案和解析>>
科目:初中数学 来源:2012-2013学年江苏省泰州市九年级下学期第二次涂卡训练数学试卷(解析版) 题型:解答题
如图,已知关于 的一元二次函数
的一元二次函数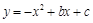 (
( )的图象与
)的图象与 轴相交于
轴相交于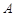 、
、 两点(点
两点(点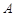 在点
在点 的左侧),与
的左侧),与 轴交于点
轴交于点 ,且
,且 ,顶点为
,顶点为 .
.

(1)求出一元二次函数的关系式;
(2)点 为线段
为线段 上的一个动点,过点
上的一个动点,过点 作
作 轴的垂线
轴的垂线 ,垂足为
,垂足为 .若
.若 ,
, 的面积为
的面积为 ,求
,求 关于
关于 的函数关系式,并写出
的函数关系式,并写出 的取值范围;
的取值范围;
(3)在(2)的条件下,当 点坐标是 时,
点坐标是 时, 为直角三角形.
为直角三角形.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com