
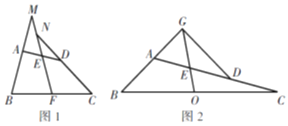
【题目】(1)如图1,在四边形ABCD中,F、E分别是BC、AD的中点,连结EF并延长,分别与BA、CD的延长线交于点M、N,则∠BME=∠CNE,求证:AB=CD;(提示取BD的中点H,连结FH,HE作辅助线)
(2)如图2,在△ABC中,且O是BC边的中点,D是AC边上一点,E是AD的中点,直线OE交BA的延长线于点G,若AB=DC=5,∠OEC=60°,求OE的长度.
【答案】(1)证明见解析;(2)OE=![]() .
.
【解析】
(1)连结BD,取DB的中点H,连结EH、FH,证明出EH∥AB,EH=![]() AB,FH∥CD,FH=
AB,FH∥CD,FH=![]() CD,证出HE=HF,进而证出AB=CD;
CD,证出HE=HF,进而证出AB=CD;
(2)连结BD,取DB的中点H,连结EH、OH,证明出HO=HE,可证明证出△OEH是等边三角形,进而求出OE=![]() .
.
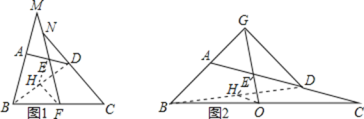
(1) 证明:如图一,连结BD,取DB的中点H,连结EH、FH.
∵E、F分别是AD、BC的中点,
∴EH∥AB,EH=![]() AB,FH∥CD,FH=
AB,FH∥CD,FH=![]() CD,
CD,
∵∠BME=∠CNE,
∴∠HEF=∠HFE,
∴HE=HF,
∴AB=CD;
(2) 如图二,连结BD,取DB的中点H,连结EH、OH,
∵AB=CD,HE为△ABD的中位线,HO为△BCD的中位线,
∴HO=HE=![]() AB=
AB=![]() CD,,
CD,,
∴∠HOE=∠HEO,
∵OH∥AC,∠OEC=60°,
∴∠OEH=∠HOE=∠OEC=60°,
∴△OEH是等边三角形,
∵AB=DC=5,
∴OE=![]() .
.
故答案为:(1)证明见解析;(2)OE=![]() .
.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】点燃一根蜡烛后,蜡烛的高度h(厘米)与燃烧时间t(分)之间的关系如下表:
t/分 | 0 | 2 | 4 | 6 | 8 | 10 |
h/厘米 | 30 | 29 | 28 | 27 | 26 | 25 |
写出蜡烛的高度h(厘米)与燃烧时间t(分)之间的关系式_____;这根蜡烛最多能燃烧的时间为_____分.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知A,B两点在直线m上,C,D两点在直线n上,∠BAD=α,∠BCD=β.
(1)如图1,若∠BAD=∠ADC,求证∠ABC=∠BCD.
(2)如图2,m∥n,过点D作DE⊥BC于点E,∠BAD与∠DEB的角平分线相交于点P,求∠P(用α,β的式子表示)
(3)在(2)的条件下,若点A沿直线m向右运动,且不与B点重合,则∠APE= (用α,β的式子表示,不写证明过程).


查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某服装厂生产一种西装和领带,西装每套定价200元,领带每条定价30元。厂方在开展促销活动期间,向客户提供两种优惠方案:方案一:一套西装送一条领带; 方案二:西装和领带都按定价的90%付款。现某客户要到该服装厂购买西装20套,领带x条(x>20)。
(1)若该客户按方案①购买,需付款 元(用含x的代数式表示);若该客户按方案②购买,需付款 元(用含x的代数式表示)°
(2)若x=30,两种方案中,通过计算说明选择按哪种方案购买较为合算。
(3)当x=30时,你能给出一种更为省钱的购买方案吗?试写出你的方案,并计算出所需的钱数。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】预习了“线段、射线、直线”一节的内容后,乐乐所在的小组,对如图展开了激烈的讨论,下列说法不正确的是( )
![]()
A. 直线AB与直线BA是同一条直线
B. 射线OA与射线AB是同一条射线
C. 射线OA与射线OB是同一条射线
D. 线段AB与线段BA是同一条线段
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】按照下面的步骤计算:
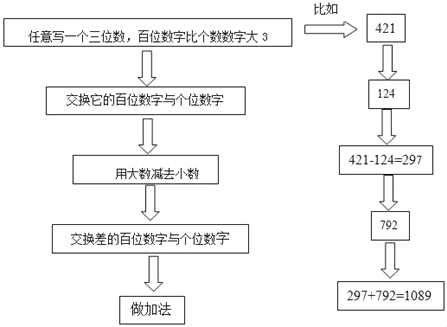
任意写一个三位数,百位数字比个数数字大3交换差的百位数字与个位数字用大数减去小数交换它的百位数字与个位数字做加法
问题:(1)用不同的三位数再做两次,结果都是1089吗?
(2)你能解释其中的道理吗?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知下列命题中为真命题的是( )
① ![]() 的算术平方根是4;
的算术平方根是4;
②若ma2>na2 , 则m>n;
③正八边形的一个内角的度数是135°;
④对角线互相垂直平分的四边形是菱形;
⑤平分弦的直径垂直于弦.
A.①③④
B.②③⑤
C.①④⑤
D.②③④
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点D,E分别在线段AB,AC上,CD与BE相交于点O,已知AB=AC,那么添加下列一个条件后,仍无法判定![]() 的是( )
的是( )
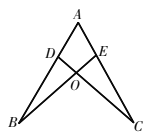
A. ![]() B. AD=AE C. BE=CD D. BD=CE
B. AD=AE C. BE=CD D. BD=CE
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com