
【题目】平面直角坐标系xOy中,已知A(﹣1,0)、B(3,0)、C(0,﹣1)三点,D(1,m)是一个动点,当△ACD的周长最小时,△ABD的面积为( )
A.![]()
B.![]()
C.![]()
D.![]()
科目:初中数学 来源: 题型:
【题目】如图,已知A(﹣2,4),B(4,2),C(2,﹣1)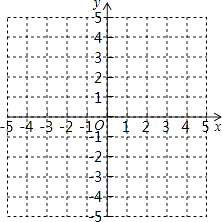
(1)作△ABC关于x轴的对称图形△A1B1C1 , 写出点C关于x轴的对称点C1的坐标;
(2)P为x轴上一点,请在图中画出使△PAB的周长最小时的点P并直接写出此时点P的坐标(保留作图痕迹).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】关于正比例函数y=2x的图象,下列叙述错误的是( )
A. 点(﹣1,﹣2)在这个图象上 B. 函数值y随自变量x的增大而减小
C. 图象关于原点对称 D. 图象经过一、三象限
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某商场销售A,B两种品牌的教学设备,这两种教学设备的进价和售价如下表所示.
A | B | |
进价(万元/套) | 1.5 | 1.2 |
售价(万元/套) | 1.65 | 1.4 |
设商场计划购进两种教学设备若干套,共需66万元,全部销售后可获毛利润9万元(毛利润=(售价-进价)×销售量).
(1)该商场计划购进A,B两种品牌的教学设备各多少套?
(2)通过市场调研,该商场决定在原计划的基础上,减少A种设备的购进数量,增加B种设备的购进数量,已知B种设备增加的数量是A种设备减少的数量的1.5倍.若用于购进这两种教学设备的总资金不超过69万元,问A种设备购进数量至多减少多少套?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某大型企业为了保护环境,准备购买A、B两种型号的污水处理设备共8台,用于同时治理不同成分的污水,若购进A型2台、B型3台需54万元,购买A型4台、B型2台需68万元.
(1)求出A型、B型污水处理设备的单价;
(2)经核实,一台A型设备一个月可处理污水220吨,一台B型设备一个月可处理污水190吨,如果该企业每月的污水处理量不低于1 565吨,请你为该企业设计一种最省钱的购买方案.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在矩形ABCD中,AD= ![]() AB,∠BAD的平分线交BC于点E,DH⊥AE于点H,连接BH并延长交CD于点F,连接DE交BF于点O,下列结论:①∠AED=∠CED;②AB=HF,③BH=HF;④BC﹣CF=2HE;⑤OE=OD;其中正确结论的序号是
AB,∠BAD的平分线交BC于点E,DH⊥AE于点H,连接BH并延长交CD于点F,连接DE交BF于点O,下列结论:①∠AED=∠CED;②AB=HF,③BH=HF;④BC﹣CF=2HE;⑤OE=OD;其中正确结论的序号是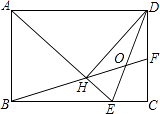
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在△ABC中,AB=15,BC=14,AC=13,求△ABC的面积.
某学习小组经过合作交流,给出了下面的解题思路,请你按照他们的解题思路完成解答过程.
(1)作AD⊥BC于D,设BD = x,用含x的代数式表示CD;
(2)根据勾股定理,利用AD作为“桥梁”,建立方程模型,求出x;
(3)利用勾股定理求出AD的长,再计算三角形面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:等边△ABC的边长为4,点P在线段AB上,点D在线段AC上,且△PDE为等边三角形,当点P与点B重合时(如图1),AD+AE的值为 ;
[类比探究]在上面的问题中,如果把点P沿BA方向移动,使PB=1,其余条件不变(如图2),AD+AE的值是多少?请写出你的计算过程;
[拓展迁移]如图3,△ABC中,AB=BC,∠ABC=a,点P在线段BA延长线上,点D在线段CA延长线上,在△PDE中,PD=PE,∠DPE=a,设AP=m,则线段AD、AE有怎样的等量关系?请用含m,a的式子直接写出你的结论.
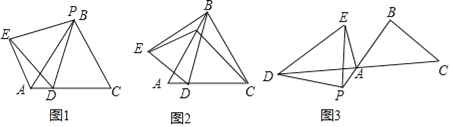
查看答案和解析>>
科目:初中数学 来源: 题型:
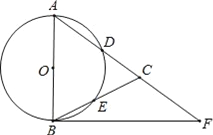
【题目】如图,在△ABC,AB=AC,以AB为直径的⊙O分别交AC、BC于点D、E,点F在AC的延长线上,且∠CBF=![]() ∠CAB.
∠CAB.
(1)求证:直线BF是⊙O的切线;
(2)若AB=5,sin∠CBF=![]() ,求BC和BF的长.
,求BC和BF的长.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com