
【题目】某校学生会向全校2400名学生发起了爱心捐款活动,为了解捐款情况,学生会随机调查了部分学生的捐款金额,并用得到的数据绘制了如下统计图1和图2,请根据相关信息,解答系列问题:
(1)本次接受随机抽样调查的学生人数为 人,图1中m的值是 ;
(2)求本次调查获取的样本数据的平均数和中位数;
(3)根据样本数据,估计该校本次活动捐款金额为10元的学生人数.

【答案】(1)50,32;(2)16,15;(3)768.
【解析】
(1)根据题意由5元的人数及其所占百分比可得抽样调查的学生人数,用10元人数除以抽样调查的学生人数可得m的值;
(2)由题意根据统计图可以分别得到本次调查获取的样本数据的平均数和中位数;
(3)由题意根据全校总人数捐款金额为10元的学生人数所占乘以抽样调查的学生人数的比例,即可估计该校本次活动捐款金额为10元的学生人数.
解:(1)本次接受随机抽样调查的学生人数为4÷8%=50人,
∵![]() ,
,
![]() .
.
故答案为:50;32.
(2)本次调查获取的样本数据的平均数是:![]() (元);
(元);
本次调查获取的样本数据的中位数是:15元.
(3)估计该校本次活动捐款金额为10元的学生人数为2400×32%=768人.


科目:初中数学 来源: 题型:
【题目】二次函数y=ax2+bx+c (a、b、c为常数且a≠0)中的x与y的部分对应值如下表,
x | … | -3 | -2 | -1 | 0 | 1 | 2 | 3 | 4 | 5 | … |
y | … | 12 | 5 | 0 | -3 | -4 | -3 | 0 | 5 | 12 | … |
下列四个结论:
(1)二次函数y=ax2+bx+c 有最小值,最小值为-3;
(2)抛物线与y轴交点为(0,-3);
(3)二次函数y=ax2+bx+c 的图像对称轴是x=1;
(4)本题条件下,一元二次方程ax2+bx+c的解是x1=-1,x2=3.
其中正确结论的个数是( )
A. 4 B. 3 C. 2 D. 1
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系![]() 中,已知一次函数
中,已知一次函数![]() =
=![]() 的图象经过点A(1,0),与反比例函数
的图象经过点A(1,0),与反比例函数![]() =
=![]() (
(![]() >0)的图象相交于点B(m,1).
>0)的图象相交于点B(m,1).
(1)求m的值和一次函数的解析式;
(2)结合图象直接写出:当![]() >0时,不等式
>0时,不等式![]() >
>![]() 的解集.
的解集.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,⊙O中,直径CD⊥弦AB于M,AE⊥BD于E,交CD于N,连AC
(1)求证:AC=AN;
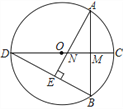
(2)若OM∶OC=3∶5,AB=5,求⊙O的半径;
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,∠C=90°,∠B=30°,以A为圆心,任意长为半径画弧分别交AB、AC于点M和N,再分别以M、N为圆心,大于MN的长为半径画弧,两弧交于点P,连结AP并延长交BC于点D,则下列说法中正确的个数是
①AD是∠BAC的平分线;②∠ADC=60°;③点D在AB的中垂线上;④S△DAC:S△ABC=1:3.

A.1 B.2 C.3 D.4
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】我国魏晋时期数学家刘徽编撰的最早一部测量数学著作《海岛算经》中有一题:今有望海岛,立两表齐高三丈,前后相去千步,令后表与前表参相直.从前表却行一百二十三步,人目着地,取望岛峰,与表末参合.从后表却行一百二十七步,人目着地,取望岛峰,亦与表末参合.问岛高几何?

译文:今要测量海岛上一座山峰AH的高度,在B处和D处树立标杆BC和DE,标杆的高都是3丈,B和D两处相隔1000步(1丈=10尺,1步=6尺),并且AH,CB和DE在同一平面内.从标杆BC后退123步的F处可以看到顶峰A和标杆顶端C在同一直线上;从标杆ED后退127步的G处可以看到顶峰A和标杆顶端E在同一直线上.则山峰AH的高度是_______.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,方格纸中的每个小方格都是边长为1个单位的正方形,在建立平面直角坐标系后,△ABC的顶点均在格点上,点B的坐标为(1,0).
(1)在图1中画出△ABC关于y轴对称的△A1B1C1,直接写出点C的对应点C1的坐标.
(2)在图2中,以点O为位似中心,将△ABC放大,使放大后的△A2B2C2与△ABC的对应边的比为2:1(画出一种即可).直接写出点C的对应点C2的坐标.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读理解
如图 a,在△ABC 中,D 是 BC 的中点.如果用 SABC 表示△ABC 的面积,则由等底等高的三角形的面积相等,可得![]()
![]()
![]()
![]() .同理,如图 b,在 ABC 中,D、E 是 BC 的三等分点,可得
.同理,如图 b,在 ABC 中,D、E 是 BC 的三等分点,可得![]()
![]()
![]()
![]()
![]()

结论应用
已知△ABC 的面积为 42,请利用上面的结论解决下列问题:


(1)如图 1,若 D、E 分别是 AB、AC 的中点,CD 与 BE交于点 F,则△DBF 的面积为 ;
类比推广
(2)如图 2,若 D、E 是 AB 的三等分点,F、G 是 AC 的 三等分点,CD 分别交 BF、BG 于 M、N,CE 分别交 BF、BG 于 P、Q,求△BEP 的面积;
(3)如图2,问题(2)中的条件不变,求四边形EPMD的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】动手操作:
如图,已知AB∥CD,点A为圆心,小于AC长为半径作圆弧,分别交AB,AC于E,F两点,再分别以点E,F为圆心,大于![]() EF长为半径作圆弧,两条圆弧交于点P,作射线AP,交CD于点M.
EF长为半径作圆弧,两条圆弧交于点P,作射线AP,交CD于点M.
问题解决:
(1)若∠ACD=78°,求∠MAB的度数;
(2)若CN⊥AM,垂足为点N,求证:△CAN≌△CMN.
实验探究:
(3)直接写出当∠CAB的度数为多少时?△CAM分别为等边三角形和等腰直角三角形.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com