
 x2上,DC交y轴于N点,一条直线OE与AB交于E点,与DC交于F点,如果E点的横坐标为a,四边形ADFE的面积为
x2上,DC交y轴于N点,一条直线OE与AB交于E点,与DC交于F点,如果E点的横坐标为a,四边形ADFE的面积为 .
.
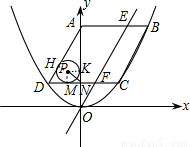
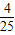 x2上
x2上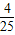 x2上,且CD∥x轴
x2上,且CD∥x轴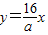
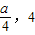 )
)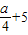 且S梯形ADFE=
且S梯形ADFE=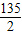 ,
, (5+12+13)r=
(5+12+13)r= ×5×12,r=2
×5×12,r=2 =
=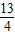
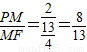 .
.

 全能测控期末小状元系列答案
全能测控期末小状元系列答案科目:初中数学 来源:2007年全国中考数学试题汇编《二次函数》(07)(解析版) 题型:解答题
 x2上,DC交y轴于N点,一条直线OE与AB交于E点,与DC交于F点,如果E点的横坐标为a,四边形ADFE的面积为
x2上,DC交y轴于N点,一条直线OE与AB交于E点,与DC交于F点,如果E点的横坐标为a,四边形ADFE的面积为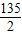 .
.
查看答案和解析>>
科目:初中数学 来源:2009年陕西省中考模拟数学试卷(4)(金台中学 杨宏举)(解析版) 题型:解答题
 x2上,DC交y轴于N点,一条直线OE与AB交于E点,与DC交于F点,如果E点的横坐标为a,四边形ADFE的面积为
x2上,DC交y轴于N点,一条直线OE与AB交于E点,与DC交于F点,如果E点的横坐标为a,四边形ADFE的面积为 .
.
查看答案和解析>>
科目:初中数学 来源:2009年江苏省无锡市宜兴市初三数学适应性练习(解析版) 题型:解答题
 x2上,DC交y轴于N点,一条直线OE与AB交于E点,与DC交于F点,如果E点的横坐标为a,四边形ADFE的面积为
x2上,DC交y轴于N点,一条直线OE与AB交于E点,与DC交于F点,如果E点的横坐标为a,四边形ADFE的面积为 .
.
查看答案和解析>>
科目:初中数学 来源:2007年四川省内江市中考数学试卷(解析版) 题型:解答题
 x2上,DC交y轴于N点,一条直线OE与AB交于E点,与DC交于F点,如果E点的横坐标为a,四边形ADFE的面积为
x2上,DC交y轴于N点,一条直线OE与AB交于E点,与DC交于F点,如果E点的横坐标为a,四边形ADFE的面积为 .
.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com