
���� ��1�����������0���г�����ʽ���ⲻ��ʽ���ɣ�
��2���������ۣ�ƽ�ƺ��ͼ���ݶ������꼴��д�������Ľ���ʽ��
��3������ȷ��n��ȡֵ��Χ�����ö��κ��������ʼ��ɽ�����⣻
��� �⣺��1������һԪ���η���x2-��m+1��x+$\frac{1}{2}$��m2+1��=0��
��=��m+1��2-2��m2+1��=-m2+2m-1=-��m-1��2��
�߷�����ʵ������
��-��m-1��2��0��
��m=1��
��2���ɣ�1����֪y=x2-2x+1=��x-1��2��
ͼ����ͼ��ʾ��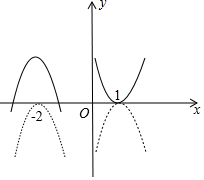
ƽ�ƺ�Ľ���ʽΪy=-��x+2��2+2=-x2-4x-2��
��3����$\left\{\begin{array}{l}{y=2x+n}\\{y=-{x}^{2}-4x-2}\end{array}\right.$��ȥy�õ�x2+6x+n+2=0��
���������0��
��36-4n-8��0��
��n��7��
��n��m��m=1��
��1��n��7��
��y��=n2-4n=��n-2��2-4��
��n=2ʱ��y���ֵ��С����СֵΪ-4��
n=7ʱ��y���ֵ������ֵΪ21��
��n2-4n�����ֵΪ21����СֵΪ-4��
���� ���⿼����������x��Ľ��㡢����ϵ���������۱任��ƽ�Ʊ任�����κ�������ֵ�����֪ʶ������Ĺؼ����������⣬ѧ����ת����˼��˼�����⣬�����п��������ͣ�



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
| A�� | 140��x��150 |
| B�� | 130��x��140 |
| C�� | 120��x��130 |
| D�� | 110��x��120 |
| E�� | 100��x��110 |
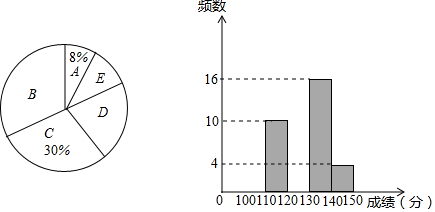
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | x��2 | B�� | x��2 | C�� | x=-1 | D�� | x=2 |
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com