
 新活力总动员暑系列答案
新活力总动员暑系列答案 龙人图书快乐假期暑假作业郑州大学出版社系列答案
龙人图书快乐假期暑假作业郑州大学出版社系列答案科目:初中数学 来源: 题型:
 (2013•宁化县质检)已知:如图,抛物线y=ax2+bx+c与x轴交于点A(1-
(2013•宁化县质检)已知:如图,抛物线y=ax2+bx+c与x轴交于点A(1-| 3 |
| ||
| 2 |
| 5 |
| 6 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 已知:如图,抛物线y=ax2+bx+c与x轴交于点A(
已知:如图,抛物线y=ax2+bx+c与x轴交于点A(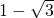 ,0)和点B,将抛物线沿x轴向上翻折,顶点P落在点P′(1,3)处.
,0)和点B,将抛物线沿x轴向上翻折,顶点P落在点P′(1,3)处. (约等于0.618).请你计算这个“W”图案的高与宽的比到底是多少?(参考数据:
(约等于0.618).请你计算这个“W”图案的高与宽的比到底是多少?(参考数据: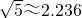 ,
,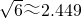 ,结果精确到0.001)
,结果精确到0.001)查看答案和解析>>
科目:初中数学 来源:2013年福建省三明市宁化县初中学业质量检查数学试卷(解析版) 题型:解答题
 ,0)和点B,将抛物线沿x轴向上翻折,顶点P落在点P′(1,3)处.
,0)和点B,将抛物线沿x轴向上翻折,顶点P落在点P′(1,3)处.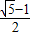 (约等于0.618).请你计算这个“W”图案的高与宽的比到底是多少?(参考数据:
(约等于0.618).请你计算这个“W”图案的高与宽的比到底是多少?(参考数据: ,
, ,结果精确到0.001)
,结果精确到0.001)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com