
 如图,在△ABC中,AD为边BC上的中线,延长AD的到E,使得DE=AD,连接BE
如图,在△ABC中,AD为边BC上的中线,延长AD的到E,使得DE=AD,连接BE分析 (1)首先证得△BDE≌△CAD,再进一步得出答案即可;
(2)四边形ABEC是平行四边形,由此直接得出与△ABC的面积相等的三角形即可.
解答 解:(1)△ABC与△ABE的面积相等.
理由:∵AD为边BC上的中线,
∴BD=CD,
在△BDE和△CAD中,
$\left\{\begin{array}{l}{BD=DC}\\{∠BDE=∠CDA}\\{DE=AD}\end{array}\right.$,
∴△BDE≌△CAD,
∴S△BDE+S△ABD=S△CAD+S△ABD,
即△ABC与△ABE的面积相等.
(2)如图,
∵△BDE≌△CAD,
∴BE=AC,∠DBE=∠DCA,
∴BE∥AC,
∴四边形ABEC是平行四边形,
∴与△ABC的面积相等的三角形有△AEC、△BCE、△ABE.
点评 此题考查三角形的面积,掌握等底等高三角形的面积相等是解决问题的关键.


科目:初中数学 来源: 题型:解答题
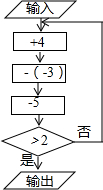 如图是一个数值转换机,输入数值后按三个方框中的程序运算,若第一次运算结果大于2,可以输出结果,则称该数只要“算一遍”;若第一次运算无法输出结果,且第二次运算结果大于2,可以输出结果,则称该数需要“算两遍”,以此类推:
如图是一个数值转换机,输入数值后按三个方框中的程序运算,若第一次运算结果大于2,可以输出结果,则称该数只要“算一遍”;若第一次运算无法输出结果,且第二次运算结果大于2,可以输出结果,则称该数需要“算两遍”,以此类推:查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,在等边△ABC中,点D,E分别在边BC,AC上,且DE∥AB,过点E作EF⊥DE,交BC的延长线于点F,
如图,在等边△ABC中,点D,E分别在边BC,AC上,且DE∥AB,过点E作EF⊥DE,交BC的延长线于点F,查看答案和解析>>
科目:初中数学 来源: 题型:解答题
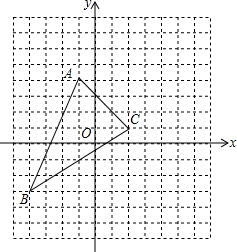 如图,将三角形ABC向右平移5个单位长度,再向上平移3个单位长度,请解答下列问题:
如图,将三角形ABC向右平移5个单位长度,再向上平移3个单位长度,请解答下列问题:查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 5条 | B. | 4条 | C. | 3条 | D. | 2条 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
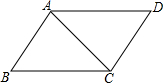 我们知道平行四边形的一条对角线把这个平行四边形分成两个全等的三角形.如图,请你用“≌”表示这两个全等三角形,并写出图中相等的边和相等的角.
我们知道平行四边形的一条对角线把这个平行四边形分成两个全等的三角形.如图,请你用“≌”表示这两个全等三角形,并写出图中相等的边和相等的角.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
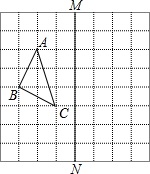 如图,在正方形网格中,每个小正方形的边长都为1,网格中有一个格点△ABC(即三角形的顶点都在格点上).
如图,在正方形网格中,每个小正方形的边长都为1,网格中有一个格点△ABC(即三角形的顶点都在格点上).查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com