
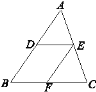
【题目】如图,点D,E分别在AB,AC上,DE∥BC,EF平分∠DEC,交BC于点F,且∠ABC=55°,∠C=70°.
(1)求∠DEF的度数;
(2)请判断EF与AB的位置关系,并说明理由.
科目:初中数学 来源: 题型:
【题目】计算:
(1)(-3pq)2;
(2)-x3+(-4x)2x;
(3)(m4m÷m2n)·mn;
(4)(-2)-2-32÷(3.144+π)0;
(5)(a2)3·(a2)4÷(-a2)5;
(6)[-2-3-8-1×(-1)-2]×![]() .
.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(1)如图(1),已知:在△ABC中,∠BAC=90°,AB=AC,直线m经过点A,BD⊥直线m, CE⊥直线m,垂足分别为点D、E.证明:DE=BD+CE.
(2) 如图(2),将(1)中的条件改为:在△ABC中,AB=AC,D、A、E三点都在直线m上,并且有∠BDA=∠AEC=∠BAC=![]() ,其中
,其中![]() 为任意锐角或钝角.请问结论DE=BD+CE是否成立?如成立,请你给出证明;若不成立,请说明理由.
为任意锐角或钝角.请问结论DE=BD+CE是否成立?如成立,请你给出证明;若不成立,请说明理由.
(3)拓展与应用:如图(3),D、E是D、A、E三点所在直线m上的两动点(D、A、E三点互不重合),点F为∠BAC平分线上的一点,且△ABF和△ACF均为等边三角形,连接BD、CE,若∠BDA=∠AEC=∠BAC,试判断△DEF的形状.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】我们知道不等式的两边加(或减)同一个数(或式子),不等号的方向不变.不等式组是否也具有类似的性质呢?请解答下列问题.
(1)完成下列填空:
已知 | 用“<”或“>”填空 |
| 5+2_____3+1 |
| ﹣3﹣1_____﹣5﹣2 |
| 1﹣2_____4+1 |
(2)一般地,如果![]() 那么a+c_____b+d(用“<”或“>”填空).请你说明上述性质的正确性.
那么a+c_____b+d(用“<”或“>”填空).请你说明上述性质的正确性.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,A(﹣1,5),B(﹣1,0),C(﹣4,3).
(1)求出△ABC的面积;
(2)在图中作出△ABC关于y轴的对称图形△A1B1C1;
(3)写出点A1,B1,C1的坐标.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,点D是BC边上的一点,∠B=44°,∠BAD=28°,将△ABD沿AD折叠得到△AED,AE与BC交于点F.
(1)填空:∠AFC= 度;
(2)求∠EDF的度数.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某天放学后,小红步行,小丽骑自行车沿同一条笔直的马路到图书馆看书,图中线段OA、BC分别表示小红、小丽离开学校的路程s(米)与小红所用的时间t(分钟)的函数关系,根据图象解答下列问题:
(1)小丽比小红迟出发 分钟,小红步行的速度是 米/分钟;(直接写出结果)
(2)两人在路上相距不超过200米的时间有多少分钟?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】直线![]() 经过原点和点
经过原点和点![]() ,点
,点![]() 的坐标为
的坐标为![]() .
.
(1)求直线![]() 所对应的函数解析式;
所对应的函数解析式;
(2)当P在线段OA上时,设![]() 点横坐标为
点横坐标为![]() ,三角形
,三角形![]() 的面积为
的面积为![]() ,写出
,写出![]() 关于
关于![]() 的函数解析式,并指出自变量
的函数解析式,并指出自变量![]() 的取值范围;
的取值范围;
(3)当P在射线OA上时,在坐标轴上有一点![]() ,使
,使![]() (
(![]() 正整数),请直接写出点
正整数),请直接写出点![]() 的坐标(本小题只要写出结果,不需要写出解题过程)
的坐标(本小题只要写出结果,不需要写出解题过程)

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】甲、乙两辆汽车沿同一路线赶赴距出发地480千米的目的地,乙车比甲车晚出发2小时(从甲车出发时开始计时),图中折线OABC、线段DE分别表示甲、乙两车所行路程y(千米)与时间x(小时)之间的函数关系对应的图像线段AB表示甲出发不足2小时因故停车检修),请根据图像所提供的信息,解决如下问题:
(1)求乙车所行路程y与时间x的函数关系式;
(2)求两车在途中第二次相遇时,它们距出发地的路程;
(3)乙车出发多长时间,两车在途中第一次相遇?(写出解题过程)

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com