
【题目】已知点A、B分别在反比例函数y= ![]() (x>0),y=﹣
(x>0),y=﹣ ![]() (x>0)的图象上,且OA⊥OB,则tanB为 .
(x>0)的图象上,且OA⊥OB,则tanB为 . 
【答案】![]()
【解析】解:过A作AC⊥y轴,过B作BD⊥y轴,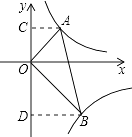
可得∠ACO=∠BDO=90°,
∴∠AOC+∠OAC=90°,
∵OA⊥OB,
∴∠AOC+∠BOD=90°,
∴∠OAC=∠BOD,
∴△AOC∽△OBD,
∵点A、B分别在反比例函数y= ![]() (x>0),y=﹣
(x>0),y=﹣ ![]() (x>0)的图象上,
(x>0)的图象上,
∴S△AOC=1,S△OBD=4,
∴S△AOC:S△OBD=1:4,即OA:OB=1:2,
则在Rt△AOB中,tan∠ABO= ![]() .
.
故答案为: ![]()
过A作AC垂直于y轴,过B作BD垂直于y轴,利用垂直的定义可得出一对直角相等,再由OA与OB垂直,利用平角的定义得到一对角互余,在直角三角形AOC中,两锐角互余,利用同角的余角相等得到一对角相等,利用两对对应角相等的三角形相似得到三角形AOC与三角形OBD相似,利用反比例函数k的几何意义求出两三角形的面积,得出面积比,利用面积比等于相似比的平方求出相似比,即为OA与OB的比值,在直角三角形AOB中,利用锐角三角函数定义即可求出tan∠ABO的值.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】如图,一个长5m的梯子AB,斜靠在一竖直的墙AO上,这时AO的距离为4m,如果梯子的顶端A沿墙下滑1m至C点.
(1)求梯子底端B外移距离BD的长度;
(2)猜想CE与BE的大小关系,并证明你的结论.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC的三边AB、BC、CA长分别是20、30、40,其三条角平分线将△ABC分为三个三角形,则S△ABO︰S△BCO︰S△CAO等于( )

A. 1︰1︰1
B. 1︰2︰3
C. 2︰3︰4
D. 3︰4︰5
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】计算:
(1)5m-7n-8p+5n-9m-p;
(2)x4x5(-x)7+5(x4)4-(x7)3÷x5.
【答案】(1)-4m-2n-9p;(2)3x16
【解析】
(1)先移项,再合并同类项;
(2)原式利用幂的乘方、同底数幂的乘法和除法法则计算,再合并即可得到结果.
(1)5m-7n-8p+5n-9m-p=5m-9m-7n+5n-8p-p=-4m-2n-9p;
(2)x4x5(-x)7+5(x4)4-(x7)3÷x5=- x4x5x7+5x16-x21÷x5=- x16 +5x16-x16=3x16
【点睛】
此题考查了幂的乘方、同底数幂的乘法、除法法则计算以及合并同类项,熟练掌握整式运算的有关法则是解答此题的关键.
【题型】解答题
【结束】
21
【题目】解方程:![]() (x-2)-
(x-2)-![]() (4x-1)=4.
(4x-1)=4.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,将△ABC绕点A逆时针旋转一定角度,得到△ADE,此时点C恰好在线段DE上,若∠B=40°,∠CAE=60°,则∠DAC的度数为( ) 
A.15°
B.20°
C.25°
D.30°
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(1)已知a+b=5,ab=-2,求代数式(6a-3b-2ab)-(a-8b-ab)的值;
(2)已知2x-y-4=0,求9x27y÷81y的值.
【答案】(1)27;(2)81.
【解析】
(1)运用整式的加减运算顺序先去括号,再合并同类项,根据乘法的分配律将5a+5b变形为5(a+b),最后代入求值即可;
(2)根据幂的乘方,可得同底数幂的乘法,根据同底数幂的乘法,可得答案.
(1)原式=6a-3b-2ab-a+8b+ab=5a+5b-ab=5(a+b)-ab,
当a+b=5,ab=-2时,
原式=5×5-(-2)=27;
(2)9x27y÷81y=32x33y÷34y=32x-y,
由2x-y-4=0,得2x-y=4,
故原式=34=81.
【点睛】
本题考查了幂的乘方,同底数幂的乘法,整式的混合运算和求值的应用,用了整体代入思想.
【题型】解答题
【结束】
23
【题目】根据要求完成下列题目:
(1)图中有_____块小正方体;
(2)请在下面方格纸中分别画出它的主视图、左视图和俯视图;
(3)用小正方体搭一几何体,使得它的俯视图和左视图与你在图方格中所画的图一致,若这样的几何体最少要m个小正方体,最多要n个小正方体,则m+n的值为____.
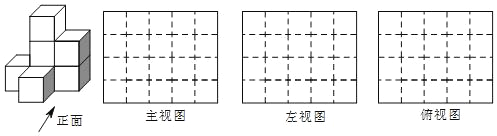
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】圆锥纸帽的侧面展开图是一个圆心角为120°,弧长为6π(cm)的扇形纸片,则圆锥形纸帽的侧面积为( )
A.9π cm2
B.18π cm2
C.27π cm2
D.36π cm2
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知直线y= ![]() x+b与双曲线y=
x+b与双曲线y= ![]() 的一个交点为(2,5),直线与y轴交于点A.
的一个交点为(2,5),直线与y轴交于点A. 
(1)求m的值及点A的坐标;
(2)若点P在双曲线y= ![]() 的图象上,且S△POA=10,求点P的坐标.
的图象上,且S△POA=10,求点P的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,路灯OP距地面8米,身高1.6米的小明从距离灯的底部(点O)20米的点A处,沿OA所在的直线行走14米到点B处时,人影的长度( ) 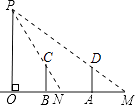
A.变长了1.5米
B.变短了2.5米
C.变长了3.5米
D.变短了3.5米
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com