Question

10．已知，点A，B分别在x轴，y轴上，K（2，2）是边AB上的一点，CK⊥AB交x轴于C．
（1）如图①，求OB+OC的值；
（2）如图②，延长KC交y轴于D，求S_△ACK-S_△OCD的值；
（3）如图③，点P为AK上任意一点（P不与A，K重合），过A作AE⊥DP于E，连EK，求∠DEK的度数．

Answer 1

分析 （1）如图①，作辅助线，构建全等三角形，先证明四边形OMKN为正方形得：OM=ON=2，再证明△KNB≌△KMC，则CM=BN，代入OB+OC中可得结论；
（2）如图②，证明△AMK≌△DNK，则S_△AMK=S_△DNK，所以S_△ACK-S_△OCD拆成和与差的形式并等量代换得结果为4；
（3）如图③，作辅助线，构建全等三角形，证明△KDF≌△KAE，得KF=KE，∠DKF=∠AKE，再得△FKE是等腰直角三角形，所以∠DEK=45°．

解答 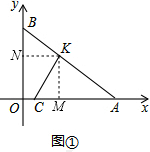解：（1）如图①，过K作KM⊥x轴，KN⊥y轴，垂足分别为M、N，
则∠KNO=∠KMO=90°，
∵∠BOA=90°，
∴四边形OMKN是矩形，
∴∠NKM=90°，
∴∠NKC+∠CKM=90°，
∵K（2，2），
∴KM=KN=2，
∴矩形OMKN是正方形，
∴OM=ON=2，
∵CK⊥AB，
∴∠BKN+∠NKC=90°，
∴∠BKN=∠CKM，
∵∠KNB=∠CMK=90°，
∴△KNB≌△KMC，
∴CM=BN，
∴OB+OC=ON+BN+OC=ON+CM+OC=ON+OM=2+2=4；
（2）如图2，∵∠AKC=∠MKN=90°，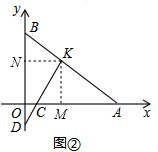
∴∠AKM=∠NKD=90°-∠CKM，
∵∠KND=∠KMA=90°，KM=KN，
∴△AMK≌△DNK，
∴S_△AMK=S_△DNK，
∴S_△ACK-S_△OCD=S_△AMK+S_△CKM-S_△OCD，
=S_△DNK+S_△CKM-S_△OCD，
=S_{正方形OMKN}+S_△OCD-S_△OCD，
=2×2，
=4．
（3）由（2）得：△AMK≌△DNK，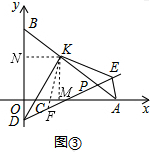
∴AK=DK，
在DE上截取DF=AE，连接KF，
∵AE⊥EF，DK⊥AB，
∴∠DKP=∠AEP=90°，
∵∠KPD=∠EPA，
∴∠KDF=∠KAE，
∴△KDF≌△KAE，
∴KF=KE，∠DKF=∠AKE，
∵∠DKP=90°，
∴∠DKF+∠FKP=∠AKE+∠FKP=∠FKE=90°，
∴△FKE是等腰直角三角形，
∴∠DEK=45°．

点评 本题是三角形的综合题，考查了全等三角形、正方形、矩形的性质和判定；以证明三角形全等为关键，利用全等三角形对应边相等和对应角相等得出边与角的关系；同时利用了全等三角形的面积也相等，在求解三角形面积的差时，利用三角形面积相等关系进行变形并加减得出与正方形的面积相等，从而得出结论．