Question

若多边形的所有内角与它的一个外角的和为600°，求边数和内角和．

Answer 1

解：设边数为n，一个外角为α，
则（n-2）•180+α=600，
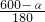
∴n=+2．
∵0°＜α＜180°，n为正整数，
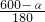
∴为整数，
∴α=60°，
∴n=5，此时内角和为（n-2）•180°=540°．
分析：由于n边形的内角和是（n-2）•180°，而多边形的外角大于0度，且小于180度，因而用600°减去一个外角的度数后，得到的内角和能够被180整除，其商加上2所得的数值，就是多边形的边数．
点评：正确理解多边形外角的大小的特点，以及多边形的内角和定理是解决本题的关键．