
 如图,某人在山坡坡脚A处测得电视塔尖点C的仰角为60°,沿山坡向上走到P处再测得点C的仰角为45°,已知OA=100米,该山坡的坡度为
如图,某人在山坡坡脚A处测得电视塔尖点C的仰角为60°,沿山坡向上走到P处再测得点C的仰角为45°,已知OA=100米,该山坡的坡度为| 1 | 2 |
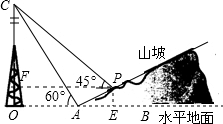 解:(1)作PE⊥OB于点E,PF⊥CO于点F,
解:(1)作PE⊥OB于点E,PF⊥CO于点F,| 3 |
| PE |
| AE |
| 1 |
| 2 |
| 3 |
| 3 |
100
| ||
| 3 |
200
| ||
| 3 |
200
| ||
| 3 |
200
| ||
| 3 |


 云南师大附小一线名师提优作业系列答案
云南师大附小一线名师提优作业系列答案科目:初中数学 来源: 题型:
| 1 |
| 2 |
| 1 |
| 2 |
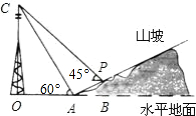 同一条直线上.求电视塔OC的高度以及此人所在位置点P的铅直高度.(测倾器的高度忽略不计,结果保留根号形式)
同一条直线上.求电视塔OC的高度以及此人所在位置点P的铅直高度.(测倾器的高度忽略不计,结果保留根号形式)查看答案和解析>>
科目:初中数学 来源: 题型:
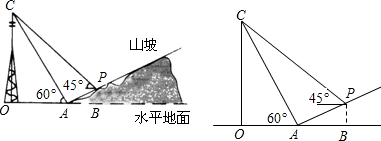
查看答案和解析>>
科目:初中数学 来源: 题型:
| 1 |
| 2 |
| 1 |
| 2 |
查看答案和解析>>
科目:初中数学 来源:2011-2012学年江苏镇江九年级5月中考模拟数学试卷(解析版) 题型:解答题
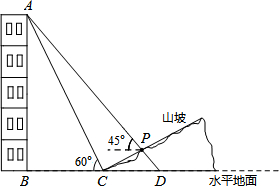
如图,某人在山坡坡脚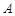 处测得电视塔尖点
处测得电视塔尖点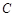 的仰角为
的仰角为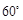 ,沿山坡向上走到
,沿山坡向上走到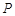 处再测得点
处再测得点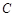 的仰角为
的仰角为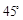 ,已知
,已知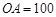 米,山坡坡度
米,山坡坡度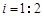 且O 、A、B在同一条直线上.求电视塔
且O 、A、B在同一条直线上.求电视塔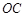 的高度以及此人所在位置点
的高度以及此人所在位置点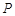 的铅直高度.(测倾器高度忽略不计,结果保留根号形式)
的铅直高度.(测倾器高度忽略不计,结果保留根号形式)

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com