练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情
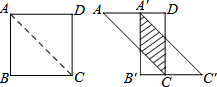
    5．如图，将边长为12cm的正方形纸片ABCD沿其对角线AC剪开，再把△ABC沿着AD方向平移，得到△A′B′C′，若两个三角形重叠部分（见图中阴影）的面积为32cm2，则它移动的距离AA′等于（　　）
    A．6cmB．8cmC．6cm或8cmD．4cm或8cm

    分析 根据平移的性质，结合阴影部分是平行四边形，△AA′H与△HCB′都是等腰直角三角形，则若设AA′=x，则阴影部分的底长为x，高A′D=12-x，根据平行四边形的面积公式即可列出方程求解．

    解答 解：设AC交A′B′于H，
    ∵∠A=45°，∠D=90°
    ∴△A′HA是等腰直角三角形
    设AA′=x，则阴影部分的底长为x，高A′D=12-x
    ∴x•（12-x）=32，
    解得x1=4，x2=8，
    即AA′=4cm或AA′=8cm
    故选：D．

    点评 本题考查了平移的性质．解决本题关键是抓住平移后图形的特点，利用方程方法解题．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：选择题

    2．如图，AD∥BC，AC=BC，∠B=65°，则∠DAC的度数为（　　）
    A．50°B．25°C．60°D．65°

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    3．如图，有一斜坡AB长170m，坡顶离地面的高度BC为80m，求此斜坡的水平距离AC的长度．

    查看答案和解析>>

    科目：初中数学 来源： 题型：填空题

    13．如图，△ABC为等腰直角三角形，∠BAC=90°，BC=1，E为直角边AB上任意一点，以线段CE为斜边作等腰Rt△CDE，连接AD，下列说法：①AC⊥ED；②∠BCE=∠ACD；③△AED∽△ECB；④AD∥BC；⑤四边形ABCD面积的最大值为$\frac{3}{8}$，其中正确的是②④⑤．

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

    20．已知二次函数y=（m-2）x2-4x+m2+2m-8的图象经过原点，则m的值为（　　）
    A．2B．-4C．2或-4D．无法确定

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    10．已知x=$\sqrt{5}+2$，y=$\sqrt{5}-2$，求下列各式的值：
    （1）x2-2xy+y2
    （2）x2-y2．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    17．如图，CD是⊙O的直径，点A在DC的延长线上，∠A=20°，AE交⊙O于点B，且AB=OC．
    （1）求∠AOB的度数．
    （2）求∠EOD的度数．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    14．若$\sqrt{{a}^{2}-2\sqrt{3}a+3}$+b2+2b+1=0，c等于$\sqrt{17}$的小数部分，求${a^2}+\frac{1}{a^2}+\frac{1}{c}-|{-b}|$的值．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    15．如图，AD是∠BAC的平分线，DE⊥AB于E，DF⊥AC于F，并且BE=CF，求证：点D在BC的垂直平分线上．

    查看答案和解析>>

    同步练习册答案