
分析 (1)求出根的判别式b2-4ac=(k-2)2-4×1×($\frac{1}{2}$k-3)=(k-3)2+7>0,即可得出结论;
(2)由根与系数的关系得出x1+x2=-(k-2),再由已知条件得出x1=3k-1,把x1代入方程得出关于k的方程,解方程即可.
解答 (1)证明:∵b2-4ac=(k-2)2-4×1×($\frac{1}{2}$k-3)
=k2-4k+4-2k+12
=k2-6k+16
=(k-3)2+7>0,
∴无论k取什么实数值,这个方程总有两个不相等的实数根.
(2)解:x1+x2=-(k-2),
2x1+x2=x1+(x1+x2)=2k+1,∴x1+2-k=2k+1,
∴x1=3k-1,
把x1代入方程得:
(3k-1)2+(k-2)(3k-1)+$\frac{1}{2}$k-3=0,
整理得:12k2-$\frac{25}{2}$k=0,
解得:k=0,或k=$\frac{25}{24}$.
点评 本题考查了根的判别式、根与系数的关系、配方法、一元二次方程的解法;熟练掌握根的判别式和根与系数的关系,并能进行推理计算是解决问题的关键.


科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
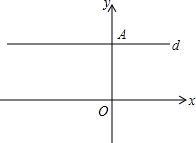 如图,在平面直角坐标系中,点O为坐标原点,A(0,a),B(b,0),a与b为方程组$\left\{\begin{array}{l}{4a+3b=-11}\\{a+b=-5}\end{array}\right.$的解,过点A作x轴的平行线d
如图,在平面直角坐标系中,点O为坐标原点,A(0,a),B(b,0),a与b为方程组$\left\{\begin{array}{l}{4a+3b=-11}\\{a+b=-5}\end{array}\right.$的解,过点A作x轴的平行线d查看答案和解析>>
科目:初中数学 来源: 题型:解答题
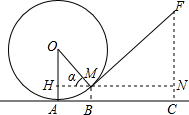 如图,圆形铁环向前滚动时,铁环钩MF保持与铁环相切,已知铁环的半径为20厘米,设铁环中心为O,铁环钩与铁环相切点为M,铁环与地面接触点为A,∠MOA=α,且sinα=$\frac{3}{5}$.
如图,圆形铁环向前滚动时,铁环钩MF保持与铁环相切,已知铁环的半径为20厘米,设铁环中心为O,铁环钩与铁环相切点为M,铁环与地面接触点为A,∠MOA=α,且sinα=$\frac{3}{5}$.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com