
【题目】如图,一次函数![]() 的图象与反比例函数
的图象与反比例函数![]() 的图象相交于
的图象相交于![]() 、
、![]() 两点,其中点
两点,其中点![]() 的坐标为
的坐标为![]() ,点
,点![]() 的坐标为
的坐标为![]() .
.

(1)根据图象,直接写出满足![]() 的
的![]() 的取值范围;
的取值范围;
(2)求这两个函数的表达式;
(3)点![]() 在线段
在线段![]() 上,且
上,且![]() ,求点
,求点![]() 的坐标.
的坐标.
【答案】(1)![]() 或
或![]() ;(2)
;(2)![]() ,
,![]() ;(3)
;(3)![]()
【解析】
(1) 观察图象得到当![]() 或
或![]() 时,直线y=k1x+b都在反比例函数
时,直线y=k1x+b都在反比例函数![]() 的图象上方,由此即可得;
的图象上方,由此即可得;
(2)先把A(-1,4)代入y=![]() 可求得k2,再把B(4,n)代入y=
可求得k2,再把B(4,n)代入y=![]() 可得n=-1,即B点坐标为(4,-1),然后把点A、B的坐标分别代入y=k1x+b得到关于k1、b的方程组,解方程组即可求得答案;
可得n=-1,即B点坐标为(4,-1),然后把点A、B的坐标分别代入y=k1x+b得到关于k1、b的方程组,解方程组即可求得答案;
(3)设![]() 与
与![]() 轴交于点
轴交于点![]() ,先求出点C坐标,继而求出
,先求出点C坐标,继而求出![]() ,根据
,根据![]() 分别求出
分别求出![]() ,
,![]() ,再根据
,再根据![]() 确定出点
确定出点![]() 在第一象限,求出
在第一象限,求出![]() ,继而求出P点的横坐标
,继而求出P点的横坐标![]() ,由点P在直线
,由点P在直线![]() 上继而可求出点P的纵坐标,即可求得答案.
上继而可求出点P的纵坐标,即可求得答案.
(1)观察图象可知当![]() 或
或![]() ,k1x+b>
,k1x+b>![]() ;
;
(2)把![]() 代入
代入![]() ,得
,得![]() ,
,
∴![]() ,
,
∵点![]() 在
在![]() 上,∴
上,∴![]() ,
,
∴![]() ,
,
把![]() ,
,![]() 代入
代入![]() 得
得
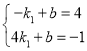 ,解得
,解得![]() ,
,
∴![]() ;
;
(3)设![]() 与
与![]() 轴交于点
轴交于点![]() ,
,
∵点![]() 在直线
在直线![]() 上,∴
上,∴![]() ,
,
![]() ,
,
又![]() ,
,
∴![]() ,
,![]() ,
,
又![]() ,∴点
,∴点![]() 在第一象限,
在第一象限,
∴![]() ,
,
又![]() ,∴
,∴![]() ,解得
,解得![]() ,
,
把![]() 代入
代入![]() ,得
,得![]() ,
,
∴![]() .
.


 通城学典默写能手系列答案
通城学典默写能手系列答案科目:初中数学 来源: 题型:
【题目】某校开展“我最喜爱的一项体育活动”调查,要求每名学生必选且只能选一项,现随机抽查了m名学生,并将其结果绘制成如下不完整的条形图和扇形图.

请结合以上信息解答下列问题:
(1)m= ;
(2)请补全上面的条形统计图;
(3)在图2中,“乒乓球”所对应扇形的圆心角的度数为 ;
(4)已知该校共有1200名学生,请你估计该校约有 名学生最喜爱足球活动.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线![]() (a≠0)的对称轴为直线x=1,与x轴的一个交点坐标为(﹣1,0),其部分图象如图所示,下列结论:
(a≠0)的对称轴为直线x=1,与x轴的一个交点坐标为(﹣1,0),其部分图象如图所示,下列结论:
①4ac<b2;
②方程![]() 的两个根是x1=﹣1,x2=3;
的两个根是x1=﹣1,x2=3;
③3a+c>0
④当y>0时,x的取值范围是﹣1≤x<3
⑤当x<0时,y随x增大而增大
其中结论正确的个数是( )

A. 4个 B. 3个 C. 2个 D. 1个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】学着说点理:补全证明过程:
如图,AB∥EF,CD⊥EF于点D,若∠B=40°,求∠BCD的度数.

解:过点C作CG∥AB.
∵AB∥EF,
∴CG∥EF.( )
∴∠GCD=∠ .(两直线平行,内错角相等)
∵CD⊥EF,
∴∠CDE=90°.( )
∴∠GCD= .(等量代换)
∵CG∥AB,
∴∠B=∠BCG.( )
∵∠B=40°,
∴∠BCG=40°.
则∠BCD=∠BCG+∠GCD= .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】数学活动 实验、猜想与证明
问题情境
(1)数学活动课上,小颖向同学们提出了这样一个问题:如图(1),在矩形ABCD中,AB=2BC,M、N分别是AB,CD的中点,作射线MN,连接MD,MC,请直接写出线段MD与MC之间的数量关系.

解决问题
(2)小彬受此问题启发,将矩形ABCD变为平行四边形,其中∠A为锐角,如图(2),AB=2BC,M,N分别是AB,CD的中点,过点C作CE⊥AD交射线AD于点E,交射线MN于点F,连接ME,MC,则ME=MC,请你证明小彬的结论;
(3)小丽在小彬结论的基础上提出了一个新问题:∠BME与∠AEM有怎样的数量关系?请你回答小丽提出的这个问题,并证明你的结论.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某商场为了吸引顾客,设立了一个可以自由转动的转盘,如图所示,并规定:顾客消费200元(含200元)以上,就能获得一次转动转盘的机会,如果转盘停止后,指针正好对准九折、八折、七折区域,顾客就可以获得此项优惠,如果指针恰好在分割线上时,则需重新转动转盘.
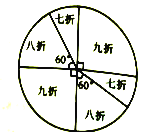
(1)某顾客正好消费220元,他转一次转盘,他获得九折、八折、七折优惠的概率分别是多少?
(2)某顾客消费中获得了转动一次转盘的机会,实际付费168元,请问他消费所购物品的原价应为多少元.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了让更多的失学儿童重返校园,某社区组织“献爱心手拉手”捐款活动,对社区部分捐款户数进行调查和分组统计后,将数据整理成如图所示的统计表和统计图(图中信息不完整).已知A、B两组捐款户数的比为1:5.
组别 | 捐款额(x)元 | 户数 |
A | 1≤x<50 | a |
B | 50≤x<100 | 10 |
C | 100≤x<150 | |
D | 150≤x<200 | |
E | x≥200 |
请结合以上信息解答下列问题.

(1)a= ,本次调查样本的容量是 ;
(2)补全“捐款户数分组统计表和捐款户数统计图1”;
(3)若该社区有1500户住户,请根据以上信息估计,全社区捐款不少于150元的户数是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】完全平方公式:(a±b)2=a2±2ab+b2适当的变形,可以解决很多的数学问题.
例如:若a+b=3,ab=1,求a2+b2的值.
解:因为a+b=3,ab=1
所以(a+b)2=9,2ab=2
所以a2+b2+2ab=9,2ab=2
得a2+b2=7
根据上面的解题思路与方法,解决下列问题:
(1)若(7﹣x)(x﹣4)=1,求(7﹣x)2+(x﹣4)2的值;
(2)如图,点C是线段AB上的一点,以AC、BC为边向两边作正方形,设AB=5,两正方形的面积和S1+S2=17,求图中阴影部分面积.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com