
【题目】已知关于x的方程x2+(m+2)x+2m-1=0.
(1)求证方程有两个不相等的实数根.
(2)当m为何值时,方程的两根互为相反数?并求出此时方程的解.
【答案】(1)证明见解析(2)x1=![]() ,x2=-
,x2=-![]()
【解析】试题分析:(1)先计算出△=(m+2)2﹣4(2m﹣1),变形得到△=(m﹣2)2+4,由于(m﹣2)2≥0,则△>0,然后根据△的意义得到方程有两个不相等的实数根;
(2)利用根与系数的关系得到x1+x2=0,即m+2=0,解得m=﹣2,则原方程化为x2﹣5=0,然后利用直接开平方法求解.
(1)证明:△=(m+2)2﹣4(2m﹣1)
=m2﹣4m+8
=(m﹣2)2+4,
∵(m﹣2)2≥0,
∴(m﹣2)2+4>0,
即△>0,
所以方程有两个不相等的实数根;
(2)设方程的两个根为x1,x2,由题意得:
x1+x2=0,即m+2=0,解得m=﹣2,
当m=﹣2时,方程两根互为相反数,
当m=﹣2时,原方程为x2﹣5=0,
解得:x1=﹣![]() ,x2=
,x2=![]() .
.


科目:初中数学 来源: 题型:
【题目】已知:如图,在菱形ABCD中,F为边BC的中点,DF与对角线AC交于点M,过M作ME⊥CD于点E,∠1=∠2.
(1)若CE=1,求BC的长;
(2)探究AM 与DF、ME有什么数量关系.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】芝麻作为食品和药物,均广泛使用,经测算,一粒芝麻重量约有0.00 000 201kg,用科学记数法表示10粒芝麻的重量为( )
A. 2.01×10﹣6kg B. 2.01×10﹣5kg C. 20.1×10﹣7kg D. 20.1×10﹣6kg
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】共享单车为市民出行带来了方便,某单车公司第一个月投放1000辆单车,计划第三个月投放单车数量比第一个月多440辆.设该公司第二、三两个月投放单车数量的月平均增长率为x,则所列方程正确的为( )
A.1000(1+x)2=1000+440
B.1000(1+x)2=440
C.440(1+x)2=1000
D.1000(1+2x)=1000+440
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知抛物线y=(x-m)2-(x-m),其中m是常数.
(1)求证:不论m为何值,该抛物线与x轴一定有两个公共点;
(2)若该抛物线的对称轴为直线x=![]() .
.
①求该抛物线的函数解析式;
②把该抛物线沿y轴向上平移多少个单位长度后,得到的抛物线与x轴只有一个公共点.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】对于二次函数![]() 和一次函数
和一次函数![]() ,把
,把![]()
![]() 称为这两个函数的“再生二次函数”,其中t是不为零的实数,其图象记作抛物线L.现有点A(2,0)和抛物线L上的点B(﹣1,n),请完成下列任务:
称为这两个函数的“再生二次函数”,其中t是不为零的实数,其图象记作抛物线L.现有点A(2,0)和抛物线L上的点B(﹣1,n),请完成下列任务:
【尝试】(1)当t=2时,抛物线![]()
![]() 的顶点坐标为 ;
的顶点坐标为 ;
(2)判断点A (填是或否)在抛物线L上;
(3)n的值是 ;
【发现】通过(2)和(3)的演算可知,对于t取任何不为零的实数,抛物线L总过定点,坐标为 .
【应用】二次函数![]() 是二次函数
是二次函数![]() 和一次函数
和一次函数![]() 的一个“再生二次函数”吗?如果是,求出t的值;如果不是,说明理由.
的一个“再生二次函数”吗?如果是,求出t的值;如果不是,说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
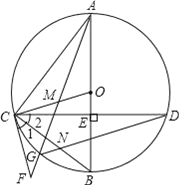
【题目】如图,在⊙O中,直径AB⊥CD,垂足为E,点M在OC上,AM的延长线交⊙O于点G,交过C的直线于F,∠1=∠2,连结CB与DG交于点N.
(1)求证:CF是⊙O的切线;
(2)求证:△ACM∽△DCN;
(3)若点M是CO的中点,⊙O的半径为4,cos∠BOC=![]() ,求BN的长.
,求BN的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,二次函数的图象交坐标轴于A(﹣1,0),B(4,0),C(0,﹣4)三点,点P是直线BC下方抛物线上一动点.
(1)求这个二次函数的解析式;
(2)动点P运动到什么位置时,△PBC面积最大,求出此时P点坐标和△PBC的最大面积.
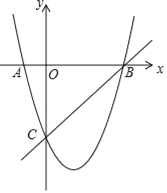
(3)是否存在点P,使△POC是以OC为底边的等腰三角形?若存在,求出P点坐标;若不存在,请说明理由;
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com