
| 单价(万元/台) | 每台处理污水量(吨/月) | |
| A型 | 12 | 220 |
| B型 | 10 | 200 |
分析 (1)设购买A型设备x台,则购买B型设备(10-x)台,根据总价=单价×数量以及工作总量=工作效率×工作时间即可得出结论;
(2)根据(1)结合购买设备的资金不超过112万元、月处理污水量不低于2080吨,即可得出关于x的一元一次不等式组,解之即可得出x的取值范围,进而即可得出各购买方案,再分别求出各购买方案的费用,比较后即可得出结论.
解答 解:(1)设购买A型设备x台,则购买B型设备(10-x)台,
根据题意得:所需资金为12x+10(10-x)=2x+100;每月处理污水总量为220x+200(10-x)=20x+2000.
故答案为:10-x;2x+100;20x+2000.
(2)根据题意得:$\left\{\begin{array}{l}{2x+100≤112}\\{20x+2000≥2080}\end{array}\right.$,
解得:4≤x≤6,
∴符合题意的购买方案有:方案一:购买A型设备4台,购买B型设备6台;方案二:购买A型设备5台,购买B型设备5台;方案三:购买A型设备6台,购买B型设备4台.
当x=4时,所需资金为2×4+100=108(万元);
当x=5时,所需资金为2×5+100=110(万元);
当x=6时,所需资金为2×6+100=112(万元).
∵108<110<112,
∴购买A型设备4台,购买B型设备6台时,所需资金最低,最低资金为108万元.
点评 本题考查了一元一次不等式组的应用,解题的关键是:(1)根据总价=单价×数量以及工作总量=工作效率×工作时间列出代数式;(2)由(1)的结论结合购买费用及处理污水量列出关于x的一元一次不等式组.


 寒假大串联黄山书社系列答案
寒假大串联黄山书社系列答案科目:初中数学 来源: 题型:选择题
| A. | 2或8 | B. | 2或-8 | C. | -2或8 | D. | -2或-8 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 三角形的三条高线相交于三角形内一点 | |
| B. | 等腰三角形一边上的中线、高线、角平分线互相重合 | |
| C. | 一条直线去截另两条直线所得的同位角相等 | |
| D. | 三角形一条边的两个顶点到这条边上的中线所在直线的距离相等 |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
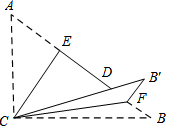 如图,Rt△ABC,∠ACB=90°,AC=3,BC=4,将边AC沿CE翻折,使点A落在AB上的点D处;再将边BC沿CF翻折,使点B落在CD的延长线上的点B'处,两条折痕与斜边AB分别交于点E、F,则线段CE的长等于$\frac{12}{5}$,线段B'F的长等于$\frac{4}{5}$.
如图,Rt△ABC,∠ACB=90°,AC=3,BC=4,将边AC沿CE翻折,使点A落在AB上的点D处;再将边BC沿CF翻折,使点B落在CD的延长线上的点B'处,两条折痕与斜边AB分别交于点E、F,则线段CE的长等于$\frac{12}{5}$,线段B'F的长等于$\frac{4}{5}$.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 4x-3(-9-3x)=3 | B. | 4x+3(-9-3x)=3 | C. | 4x-3(-9+3x)=3 | D. | 4x+3(-9+3x)=3 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com