
【题目】如图,直线y=x+2与抛物线y=ax2+bx+6(a≠0)相交于A( ![]() ,
, ![]() )和B(4,m),点P是线段AB上异于A、B的动点,过点P作PC⊥x轴于点D,交抛物线于点C.
)和B(4,m),点P是线段AB上异于A、B的动点,过点P作PC⊥x轴于点D,交抛物线于点C.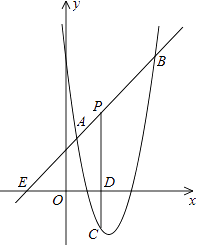
(1)求抛物线的解析式;
(2)是否存在这样的P点,使线段PC的长有最大值?若存在,求出这个最大值;若不存在,请说明理由;
(3)求△PAC为直角三角形时点P的坐标.
【答案】
(1)
解:∵B(4,m)在直线y=x+2上,
∴m=4+2=6,
∴B(4,6),
∵A( ![]() ,
, ![]() )、B(4,6)在抛物线y=ax2+bx+6上,
)、B(4,6)在抛物线y=ax2+bx+6上,
∴ 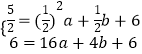 ,解得
,解得 ![]() ,
,
∴抛物线的解析式为y=2x2﹣8x+6
(2)
解:设动点P的坐标为(n,n+2),则C点的坐标为(n,2n2﹣8n+6),
∴PC=(n+2)﹣(2n2﹣8n+6),
=﹣2n2+9n﹣4,
=﹣2(n﹣ ![]() )2+
)2+ ![]() ,
,
∵PC>0,
∴当n= ![]() 时,线段PC最大且为
时,线段PC最大且为 ![]()
(3)
解:∵△PAC为直角三角形,
i)若点P为直角顶点,则∠APC=90°.
由题意易知,PC∥y轴,∠APC=45°,因此这种情形不存在;
ii)若点A为直角顶点,则∠PAC=90°.
如答图3﹣1,过点A( ![]() ,
, ![]() )作AN⊥x轴于点N,则ON=
)作AN⊥x轴于点N,则ON= ![]() ,AN=
,AN= ![]() .
.
过点A作AM⊥直线AB,交x轴于点M,则由题意易知,△AMN为等腰直角三角形,
∴MN=AN= ![]() ,∴OM=ON+MN=
,∴OM=ON+MN= ![]() +
+ ![]() =3,
=3,
∴M(3,0).
设直线AM的解析式为:y=kx+b,
则: 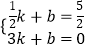 ,解得
,解得 ![]() ,
,
∴直线AM的解析式为:y=﹣x+3 ①
又抛物线的解析式为:y=2x2﹣8x+6 ②
联立①②式,解得:x=3或x= ![]() (与点A重合,舍去)
(与点A重合,舍去)
∴C(3,0),即点C、M点重合.
当x=3时,y=x+2=5,
∴P1(3,5);
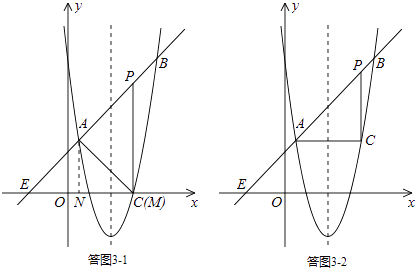
iii)若点C为直角顶点,则∠ACP=90°.
∵y=2x2﹣8x+6=2(x﹣2)2﹣2,
∴抛物线的对称轴为直线x=2.
如答图3﹣2,作点A( ![]() ,
, ![]() )关于对称轴x=2的对称点C,
)关于对称轴x=2的对称点C,
则点C在抛物线上,且C( ![]() ,
, ![]() ).
).
当x= ![]() 时,y=x+2=
时,y=x+2= ![]() .
.
∴P2( ![]() ,
, ![]() ).
).
∵点P1(3,5)、P2( ![]() ,
, ![]() )均在线段AB上,
)均在线段AB上,
∴综上所述,△PAC为直角三角形时,点P的坐标为(3,5)或( ![]() ,
, ![]() )
)
【解析】(1)已知B(4,m)在直线y=x+2上,可求得m的值,抛物线图象上的A、B两点坐标,可将其代入抛物线的解析式中,通过联立方程组即可求得待定系数的值.(2)要弄清PC的长,实际是直线AB与抛物线函数值的差.可设出P点横坐标,根据直线AB和抛物线的解析式表示出P、C的纵坐标,进而得到关于PC与P点横坐标的函数关系式,根据函数的性质即可求出PC的最大值.(3)当△PAC为直角三角形时,根据直角顶点的不同,有三种情形,需要分类讨论,分别求解.
【考点精析】根据题目的已知条件,利用二次函数的图象和二次函数的性质的相关知识可以得到问题的答案,需要掌握二次函数图像关键点:1、开口方向2、对称轴 3、顶点 4、与x轴交点 5、与y轴交点;增减性:当a>0时,对称轴左边,y随x增大而减小;对称轴右边,y随x增大而增大;当a<0时,对称轴左边,y随x增大而增大;对称轴右边,y随x增大而减小.


 巧学巧练系列答案
巧学巧练系列答案科目:初中数学 来源: 题型:
【题目】某开发商要建一批住房,经调查了解,若甲、乙两队分别单独完成,则乙队完成的天数是甲队的1.5倍;若甲、乙两队合作,则需120天完成.
(1)甲、乙两队单独完成各需多少天?
(2)施工过程中,开发商派两名工程师全程监督,需支付每人每天食宿费150元.已知乙队单独施工,开发商每天需支付施工费为10000元.现从甲、乙两队中选一队单独施工,若要使开发商选甲队支付的总费用不超过选乙队的,则甲队每天的施工费最多为多少元?(总费用=施工费+工程师食宿费)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知二次函数y=ax2+bx+c的图象与x轴交于(x1 , 0),(x2 , 0)两点,且0<x1<1,1<x2<2,与y轴交于(0,﹣2).下列结论:①2a+b>1; ②a+b>2;③a﹣b<2;④3a+b>0; ⑤a<﹣1.其中正确结论的个数为( )
A.2
B.3
C.4
D.5
查看答案和解析>>
科目:初中数学 来源: 题型:
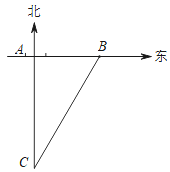
【题目】如图,一艘轮船以30km/h的速度沿既定航线由南向北航行,途中接到台风警报,某台风中心正以10km/h的速度由东向西移动,距台风中心200km的圆形区域(包括边界)都属台风影响区,当这艘轮船接到台风警报时,它与台风中心的距离BC=500km,此时台风中心与轮船既定航线的最近距离AB=300km.
(1)如果这艘船不改变航向,那么它会不会进入台风影响区?
(2)如果你认为这艘轮船会进入台风影响区,那么从接到警报开始,经过多长时间它就会进入台风影响区?
(3)假设轮船航向不变,轮船航行速度不变,求受到台风影响的时间为多少小时?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】据报道,深圳今年4 月2 日至4 月8 日每天的最高气温变化如图所示.则关于这七天的最高气温的数据,下列判断中错误的是( ) 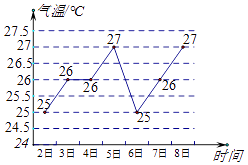
A.平均数是26
B.众数是26
C.中位数是27
D.方差是 ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
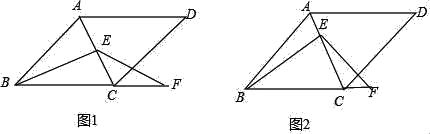
【题目】在菱形ABCD中,∠ABC=60°,E是对角线AC上任意一点,F是线段BC延长线上一点,且CF=AE,连接BE、EF.
(1)如图1,当E是线段AC的中点时,求证:BE=EF.
(2)如图2,当点E不是线段AC的中点,其它条件不变时,请你判断(1)中的结论是否成立?若成立,请证明;若不成立,说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABE中,∠A=105°,AE的垂直平分线MN交BE于点C,且AB+BC=BE,则∠B的度数是( )

A. 45° B. 60° C. 50° D. 55°
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,Rt△ABC中,AB⊥BC,AB=6,BC=4,P是△ABC内部的一个动点,且满足∠PAB=∠PBC,则线段CP长的最小值为( ) 
A.![]()
B.2
C.![]()
D.![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com