
科目:初中数学 来源: 题型:
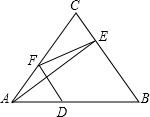 如图,△ABC的面积为18cm2,点D、E、F分别位于AB、BC、CA上.且AD=4cm,DB=5cm.如果△ABE的面积和四边形DBEF的面积相等,则△ABE的面积是( )
如图,△ABC的面积为18cm2,点D、E、F分别位于AB、BC、CA上.且AD=4cm,DB=5cm.如果△ABE的面积和四边形DBEF的面积相等,则△ABE的面积是( )| A、8cm2 | B、9cm2 | C、10cm2 | D、12cm2 |
查看答案和解析>>
科目:初中数学 来源:双色笔记九年级数学(上) 题型:044
阅读与思考:
(1)下面是课本中对平行四边形判定定理4(一组对边平行且相等的四边形是平行四边形)的证明,请边阅读,边进行推理填空,然后思考后面的问题.
已知:如图在四边形ABCD中,AB∥CD,且AB=CD.

求证:四边形ABCD是平行四边形.
证明:连结AC.
∵AB∥CD( ),
∴∠1=∠2( ),
又∵AB=CD( ),AC=AC( ),
∴△ABC≌△CDA( ),
∴BC=AD,∴四边形ABCD是平行四边形( )上面的证明是利用平行四边形判定定理________完成的.在证明过程中,证明了△ABC≌△CDA,由此还可以推出∠B=________,同理可证∠A=________,可见,平行四边形判定定理4也可以利用平行四边形判定定理________来证明.在图中再连结BD,设AC与BD相交于点O,则可以利用判定三角形全等的________公理证明△AOB≌△________,进而推出AO=________,BO=________,这说明平行四边形判定定理4也可以利用平行四边形判定定理________来证明.
(2)如果要画平行四边形ABCD,使∠B=![]() ,AB=2cm,BC=3cm,请回答下列问题:
,AB=2cm,BC=3cm,请回答下列问题:
①利用平行四边形判定定理2画所求的平行四边形ABCD,在画出AB、BC后,怎样确定点D的位置?
②利用平行四边形判定定理3画所求的平行四边形ABCD,应按怎样的步骤进行?请写出画法.
③利用平行四边形判定定理4画所求的平行四边形ABCD,在画出AB、BC后,怎样确定点D的位置?
查看答案和解析>>
科目:初中数学 来源:不详 题型:单选题
| A.四边形AEDF是平行四边形 |
| B.如果AD⊥BC,那么四边形AEDF是正方形 |
| C.如果∠BAC=90°,那么四边形AEDF是矩形 |
| D.如果AD平分∠BAC,那么四边形AEDF是菱形 |
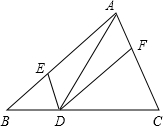
查看答案和解析>>
科目:初中数学 来源: 题型:
如图1,P为Rt△ABC所在平面内任意一点(不在直线AC上),∠ACB = 90°,M为AB边中点.

操作:以PA、PC为邻边作平行四边形PADC,连续PM并延长到点E,使ME = PM,连结DE.
探究:⑴请猜想与线段DE有关的三个结论;
⑵请你利用图2,图3选择不同位置的点P按上述方法操作;
⑶经历⑵之后,如果你认为你写的结论是正确的,请加以证明;
如果你认为你写的结论是错误的,请用图2或图3加以说明;
⑷若将“Rt△ABC”改为“任意△ABC”,其他条件不变,利用图4操作,并写出与线
段DE有关的结论(直接写答案).

图2 图3 图4
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com