
分析 (1)由于守门员从球门线出发练习折返跑,问最后是否回到了球门线的位置,只需将所有数加起来,看其和是否为0即可;
(2)计算每一次跑后的数据,绝对值最大的即为所求;
(3)求出所有数的绝对值的和即可.
解答 解:(1)(+6)+(-3)+(+11)+(-9)+(-7)+(+12)+(-10)
=(6+11+12)-(3+9+7+10)
=29-29
=0
答:守门员最后回到了球门线的位置.
(2)由观察可知:6-3+11=14米.
答:在练习过程中,守门员离开球门线最远距离是12米.
(3)|+6|+|-3|+|+11|+|-9|+|-7|+|+12|+|-10|
=6+3+11+9+7+12+10
=58米.
答:守门员全部练习结束后,他共跑了58米.
点评 本题考查了有理数的加减混合运算.关键是根据题意,正确列出算式.


 金版课堂课时训练系列答案
金版课堂课时训练系列答案 单元全能练考卷系列答案
单元全能练考卷系列答案 新黄冈兵法密卷系列答案
新黄冈兵法密卷系列答案科目:初中数学 来源: 题型:解答题
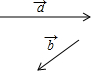 如图,已知向量$\overrightarrow{a}$、$\overrightarrow{b}$,求作$\overrightarrow{AB}$=3$\overrightarrow{a}$+2$\overrightarrow{b}$.
如图,已知向量$\overrightarrow{a}$、$\overrightarrow{b}$,求作$\overrightarrow{AB}$=3$\overrightarrow{a}$+2$\overrightarrow{b}$.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
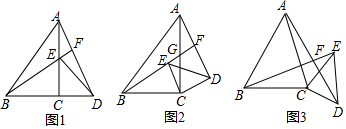
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
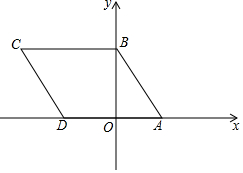 如图,边长为5的菱形ABCD如图所示放置在平面直角坐标系xOy中,点A在x轴正半轴上,点D在x轴负半轴上,点B(0,4).
如图,边长为5的菱形ABCD如图所示放置在平面直角坐标系xOy中,点A在x轴正半轴上,点D在x轴负半轴上,点B(0,4).查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com