练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    如是一元二次方程的两根，那么这就是著名的韦达定理．现在我们利用韦达定理解决问题：

       已知与是方程的两根．

       (1)填空：＝_______，＝_______；

       (2)计算的值．

    （1）3，…………………4分

       （2）

    =…………………6分

    =…………………8分

    =4…………………9分

    （其他方法请酌情给分）

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

     二次函数的图像交y轴于C点，交轴于A，B两点（点A在点B的左侧），点A、点B的横坐标是一元二次方程的两个根.（1）求出点A、点B的坐标及该二次函数表达式.

    （2）如图2，连接AC、BC，点Q是线段OB上

    一个动点（点Q不与点O、B重合），过点Q作QD∥AC交于BC点D，设Q点坐标（m，0），当面积S最大时，求m的值.

    （3）如图3，线段MN是直线y=x上的动线段（点M在点N左侧），且，若M点的横坐标为n，过点M作x轴的垂线与x轴交于点P，过点N作x轴的垂线与抛物线交于点Q.以点P，M，Q，N为顶点的四边形能否为平行四边形？若能，请求出n的值；若不能，请说明理由．

     

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    如图，已知AB是⊙O的直径，直线CD与⊙O相切于点C，AC平分∠DAB。

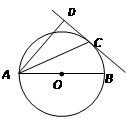
    1.求证： AD⊥DC

    2.如果AD和AC的长是一元二次方程的两根，求AD、AC、AB的长和∠DAB的度数

     

    查看答案和解析>>

    科目：初中数学 来源：2012届江苏省盐城市解放路学校中考仿真数学卷（带解析） 题型：解答题

    二次函数的图像交y轴于C点，交轴于A，B两点（点A在点B的左侧），点A、点B的横坐标是一元二次方程的两个根.（1）求出点A、点B的坐标及该二次函数表达式.

    （2）如图2，连接AC、BC，点Q是线段OB上
    一个动点（点Q不与点O、B重合），过点Q作QD∥AC交于BC点D，设Q点坐标（m，0），当面积S最大时，求m的值.
    （3）如图3，线段MN是直线y=x上的动线段（点M在点N左侧），且，若M点的横坐标为n，过点M作x轴的垂线与x轴交于点P，过点N作x轴的垂线与抛物线交于点Q.以点P，M，Q，N为顶点的四边形能否为平行四边形？若能，请求出n的值；若不能，请说明理由．

    查看答案和解析>>

    科目：初中数学 来源：2011年初中毕业升学考试（山东济南卷）数学解析版 题型：解答题

    （11·丹东）（本题14分）已知：二次函数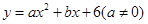与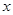轴交于A，B两点（点A在点B的左侧），点A、点B的横坐标是一元二次方程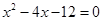的两个根.

    （1）请直接写出点A、点B的坐标.

    （2）请求出该二次函数表达式及对称轴和顶点坐标.

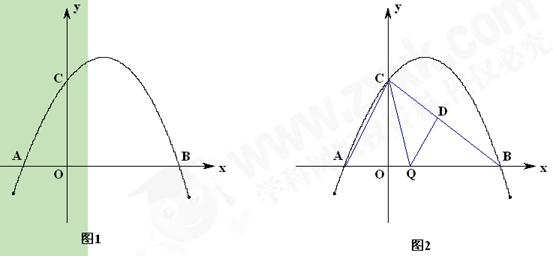
    （3）如图1，在二次函数对称轴上是否存在点P，使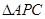的周长最小，若存在，请求出点P的坐标；若不存在，请说明理由.

    （4）如图2，连接AC、BC，点Q是线段OB上一个动点（点Q不与点O、B重合）. 过点Q作QD∥AC交于BC点D，设Q点坐标（m，0），当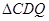面积S最大时，求m的值.

     

    查看答案和解析>>

    同步练习册答案