
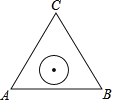
【题目】如图,若一个半径为1的圆形纸片在边长为6的等边三角形内任意运动,则在该等边三角形内,这个圆形纸片能接触到的最大面积为_____.
 世纪百通主体课堂小学课时同步达标系列答案
世纪百通主体课堂小学课时同步达标系列答案 世纪百通优练测系列答案
世纪百通优练测系列答案 百分学生作业本题练王系列答案
百分学生作业本题练王系列答案科目:初中数学 来源: 题型:
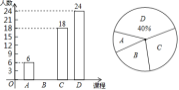
【题目】为深化课程改革,提高学生的综合素质,我校开设了形式多样的校本课程.为了解校本课程在学生中最受欢迎的程度,学校随机抽取了部分学生进行调查,从A:天文地理;B:科学探究;C:文史天地;D:趣味数学;四门课程中选你喜欢的课程(被调查者限选一项),并将调查结果绘制成两个不完整的统计图,如图所示,根据以上信息,解答下列问题:
(1)本次调查的总人数为 人,扇形统计图中A部分的圆心角是 度;
(2)请补全条形统计图;
(3)根据本次调查,该校400名学生中,估计最喜欢“科学探究”的学生人数为多少?
(4)为激发学生的学习热情,学校决定举办学生综合素质大赛,采取“双人同行,合作共进”小组赛形式,比赛题目从上面四个类型的校本课程中产生,并且规定:同一小组的两名同学的题目类型不能相同,且每人只能抽取一次,小琳和小金组成了一组,求他们抽到“天文地理”和“趣味数学”类题目的概率是多少?(请用画树状图或列表的方法求)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一个批发商销售成本为20元/千克的某产品,根据物价部门规定:该产品每千克售价不得超过90元,在销售过程中发现的售量y(千克)与售价x(元/千克)满足一次函数关系,对应关系如下表:
售价x(元/千克) | … | 50 | 60 | 70 | 80 | … |
销售量y(千克) | … | 100 | 90 | 80 | 70 | … |
(1)求y与x的函数关系式;
(2)该批发商若想获得4000元的利润,应将售价定为多少元?
(3)该产品每千克售价为多少元时,批发商获得的利润w(元)最大?此时的最大利润为多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
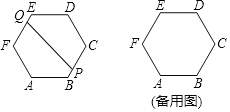
【题目】一个边长为60米的正六边形跑道,P、Q两人同时从A处开始沿相反方向都跑一圈后停止,P以4米/秒逆时针方向、Q以5米/秒顺时针方向,PQ的距离为d米,设跑步时间为x秒,令d2=y,
(1)跑道全长为 米,经过 秒两人第一次相遇.
(2)当P在BC上,Q在EF上时,求y关于x的函数解析式;并求相遇前当x为多少时,他们之间的距离最大.
(3)直接写出P、Q在整个运动过程中距离最大时的x的值及最大的距离.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知抛物线的解析式是y=x2﹣(k+2)x+2k﹣2.
(1)求证:此抛物线与x轴必有两个不同的交点;
(2)若抛物线与直线y=x+k2﹣1的一个交点在y轴上,求该二次函数的顶点坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
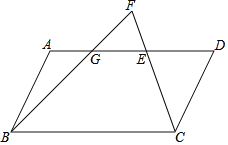
【题目】如图,在ABCD中,点E是边AD上一点,延长CE到点F,使∠FBC=∠DCE,且FB与AD相交于点G.
(1)求证:∠D=∠F;
(2)用直尺和圆规在边AD上作出一点P,使△BPC∽△CDP,并加以证明.(作图要求:保留痕迹,不写作法.)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在Rt△ABC中,∠ACB=90°,∠B=30°,AC=2,E为斜边AB的中点,点P是射线BC上的一个动点,连接AP、PE,将△AEP沿着边PE折叠,折叠后得到△EPA′,当折叠后△EPA′与△BEP的重叠部分的面积恰好为△ABP面积的四分之一,则此时BP的长为_____.
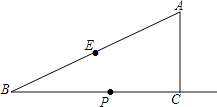
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一副直角三角板如图放置,点C在FD的延长线上,AB∥CF,∠F=∠ACB=90°,∠E=45°,∠A=60°,AC=10,则CD=_____.
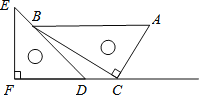
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,四边形![]() 为正方形,点
为正方形,点![]() 在
在![]() 轴上,点
轴上,点![]() 在
在![]() 轴上,且
轴上,且![]() ,
,![]() ,反比例函数
,反比例函数![]() 在第一象限的图象经过正方形的顶点
在第一象限的图象经过正方形的顶点![]() .
.

(1)求点![]() 的坐标和反比例函数的关系式.
的坐标和反比例函数的关系式.
(2)如图2,将正方形![]() 沿
沿![]() 轴向右平移 个单位长度时,点
轴向右平移 个单位长度时,点![]() 恰好落在反比例函数的图象.
恰好落在反比例函数的图象.
(3)在(2)的情况下,连接![]() 并延长,交反比例函数的图象于点
并延长,交反比例函数的图象于点![]() ,点
,点![]() 是
是![]() 轴上的一个动点(不与点
轴上的一个动点(不与点![]() 、
、![]() 重合)
重合)
①当点![]() 的坐标为多少时,四边形
的坐标为多少时,四边形![]() 是矩形?请说明理由.
是矩形?请说明理由.
②过点![]() 作
作![]() 轴于点
轴于点![]() ,请问当点
,请问当点![]() 的坐标为多少时,
的坐标为多少时,![]() 与
与![]() 相似?(直接写出答案).
相似?(直接写出答案).
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com