
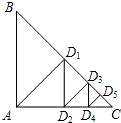
 如图,等腰Rt△ABC的直角边长为32,从直角顶点A作斜边BC的垂线交BC于D1,再从D1作D1D2⊥AC交AC于D2,再从D2作D2D3⊥BC交BC于D3,…,则AD1+D2D3+D4D5+D6D7+D8D9=________;D1D2+D3D4+D5D6+D7D8+D9D10=________.
如图,等腰Rt△ABC的直角边长为32,从直角顶点A作斜边BC的垂线交BC于D1,再从D1作D1D2⊥AC交AC于D2,再从D2作D2D3⊥BC交BC于D3,…,则AD1+D2D3+D4D5+D6D7+D8D9=________;D1D2+D3D4+D5D6+D7D8+D9D10=________. 31
31 =
= ,
, +
+ +
+ +
+ )=
)= ,
, =
=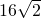 ,
, ;
; +
+ +
+ +
+ )=
)= ,
,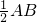 =16,
=16, .
.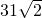 ;第二个空填31.
;第二个空填31.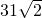 ;31.
;31.

 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:
| 2 |
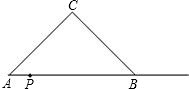 PQ=AP,以PQ为一边向上作正方形PQMN,设正方形PQMN与Rt△ABC重叠部分的面积为S.
PQ=AP,以PQ为一边向上作正方形PQMN,设正方形PQMN与Rt△ABC重叠部分的面积为S.查看答案和解析>>
科目:初中数学 来源: 题型:
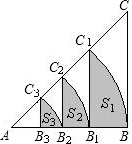 如图,等腰Rt△ABC的直角边长为4,以A为圆心,直角边AB为半径作弧BC1,交斜边AC于点C1,C1B1⊥AB于点B1,设弧BC1,C1B1,B1B围成的阴影部分的面积为S1,然后以A为圆心,AB1为半径作弧B1C2,交斜边AC于点C2,C2B2⊥AB于点B2,设弧B1C2,C2B2,B2B1围成的阴影部分的面积为S2,按此规律继续作下去,得到的阴影部分的面积S3=
如图,等腰Rt△ABC的直角边长为4,以A为圆心,直角边AB为半径作弧BC1,交斜边AC于点C1,C1B1⊥AB于点B1,设弧BC1,C1B1,B1B围成的阴影部分的面积为S1,然后以A为圆心,AB1为半径作弧B1C2,交斜边AC于点C2,C2B2⊥AB于点B2,设弧B1C2,C2B2,B2B1围成的阴影部分的面积为S2,按此规律继续作下去,得到的阴影部分的面积S3=查看答案和解析>>
科目:初中数学 来源: 题型:
 如图,等腰Rt△ABC中斜边AB=4,O是AB的中点,以O为圆心的半圆分别与两腰相切于点D、E,图中阴影部分的面积是多少?请你把它求出来.(结果用π表示)
如图,等腰Rt△ABC中斜边AB=4,O是AB的中点,以O为圆心的半圆分别与两腰相切于点D、E,图中阴影部分的面积是多少?请你把它求出来.(结果用π表示)查看答案和解析>>
科目:初中数学 来源: 题型:
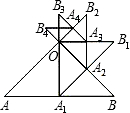 已知:如图,等腰Rt△OAB的直角边OA的长为1,以AB边上的高OA1为直角边,按逆时针方向作等腰Rt△OA1B1,A1B1与OB相交于点A2.若再以OA2为直角边按逆时针方向作等腰Rt△OA2B2,A2B2与OB1相交于点A3,按此作法进行下去,得到△OA3B3,△OA4B4,…,则△OA6B6的周长是
已知:如图,等腰Rt△OAB的直角边OA的长为1,以AB边上的高OA1为直角边,按逆时针方向作等腰Rt△OA1B1,A1B1与OB相交于点A2.若再以OA2为直角边按逆时针方向作等腰Rt△OA2B2,A2B2与OB1相交于点A3,按此作法进行下去,得到△OA3B3,△OA4B4,…,则△OA6B6的周长是查看答案和解析>>
科目:初中数学 来源: 题型:
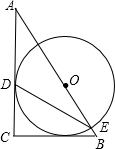 如图,等腰Rt△ABC,AC=BC,以斜边AB中点O为圆心作⊙O与AC边相切于点D,交AB于点E,连接DE.
如图,等腰Rt△ABC,AC=BC,以斜边AB中点O为圆心作⊙O与AC边相切于点D,交AB于点E,连接DE.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com