能否把正整数1至10摆放到一个圆周上，使得其中任何两个相间一个数的数的和（ai+ai+2）都是3的倍数？
【答案】
分析：假设把正整数1至10摆放到一个圆周上，能够使得其中任何两个相间一个数的数的和（a
i+a
i+2）都是3的倍数，那么这十个数之和的2倍就该是3的倍数，从而得出矛盾，进而得出结论．
解答：解：不能把正整数1到10摆放到一个圆周上，使得其中任何两个相间一个数的数和都是3的倍数．理由如下：
用a
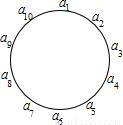
i（i=1，2，3，…，10）表示正整数1至10，将正整数1至10任意摆放到一个圆周上，如图，假设此时其中任何两个相间一个数的数的和（a
i+a
i+2）都是3的倍数，
那么a
1+a
3，a
2+a
4，a
3+a
5，a
4+a
6，a
5+a
7，a
6+a
8，a
7+a
9，a
8+a
10，a
9+a
1，a
10+a
2，都是3的倍数，
所以（a
1+a
3）+（a
2+a
4）+（a
3+a
5）+（a
4+a
6）+（a
5+a
7）+（a
6+a
8）+（a
7+a
9）+（a
8+a
10）+（a
9+a
1）+（a
10+a
2）=2（a
1+a
2+a
3+a
4+a
5+a
6+a
7+a
8+a
9+a
10）是3的倍数，
而2（a
1+a
2+a
3+a
4+a
5+a
6+a
7+a
8+a
9+a
10）=2×（1+2+3+4+5+6+7+8+9+10）=110，不是3的倍数，
所以假设不成立．
故不能把正整数1至10摆放到一个圆周上，使得其中任何两个相间一个数的数的和（a
i+a
i+2）都是3的倍数．
点评：本题考查了数的整除性，属于竞赛题型，有一定难度，根据整除的性质及已知条件得出这十个数之和的2倍就该是3的倍数是解题的关键．
