
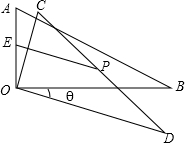
 如图,在△AOB中,∠AOB=90°,∠ABO=30°,将△AOB绕顶点O顺时针旋转,旋转角为θ(0°<θ<180°),得到△COD.设AO的中点为E,CD中点为P,AO=a,连接EP,当θ=120°时,EP长度最大,最大值为1.5a.
如图,在△AOB中,∠AOB=90°,∠ABO=30°,将△AOB绕顶点O顺时针旋转,旋转角为θ(0°<θ<180°),得到△COD.设AO的中点为E,CD中点为P,AO=a,连接EP,当θ=120°时,EP长度最大,最大值为1.5a. 分析 根据含30度的直角三角形三边的关系得到AB=2OA=2a,再根据旋转的性质CD=AB=2a,连结OP,根据直角三角形斜边上的中线性质得OP=$\frac{1}{2}$CD,如图1,根据三角形三边的关系得PE<OE+OP,点P、O、E共线时,PE=OE+OP,如图2,点Q为AB的中点,此时PE最大,易得PE的最大值为1.5a,然后求出∠AOP的度数即可得到旋转角的度数.
解答 解:∵∠AOB=90°,∠ABO=30°,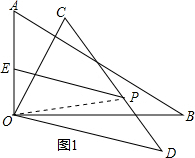
∴AB=2OA=2a,
∵△AOB绕顶点O顺时针旋转,旋转角为θ(0°<<180°)得到△COD,
∴CD=AB=2a,
连结OP,
∵CD中点为P,
∴OP=$\frac{1}{2}$CD=a,
如图1,PE<OE+OP,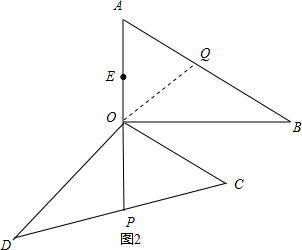 点P、O、E共线时,如图2,Q为AB的中点,
点P、O、E共线时,如图2,Q为AB的中点,
∵PE=OE+OP,
∴PE的最大值为0.5a+a=1.5a.
∵QA=QO,
∴∠AOQ=∠A=60°,
∴∠POQ=120°
∴旋转角θ=120°.
故答案为120,1.5a.
点评 本题考查了旋转的性质:对应点到旋转中心的距离相等;对应点与旋转中心所连线段的夹角等于旋转角;旋转前、后的图形全等.也考查了直角三角形斜边上的中线性质.


 海淀黄冈名师导航系列答案
海淀黄冈名师导航系列答案 普通高中同步练习册系列答案
普通高中同步练习册系列答案科目:初中数学 来源: 题型:选择题
| A. | $\frac{3}{2}$ | B. | $\frac{π}{2}$ | C. | $\frac{\sqrt{6}}{2}$ | D. | $\frac{π}{4}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
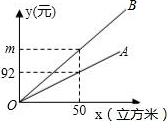 某市发改委举行居民用水价格调整听证会,届时将有两个方案提供听证.如图,射线OA、射线OB分别表示现行的、方案一的每户每月的水费y(元)与每户每月的用水量x(立方米)之间的函数关系,已知方案一的用水价比现行的用水价每立方米多0.96元;
某市发改委举行居民用水价格调整听证会,届时将有两个方案提供听证.如图,射线OA、射线OB分别表示现行的、方案一的每户每月的水费y(元)与每户每月的用水量x(立方米)之间的函数关系,已知方案一的用水价比现行的用水价每立方米多0.96元;| 阶数 | 用水量(立方米) | 用水价格(元/立方米) |
| 第一阶 | 0~15(含15)的部分 | 2.61 |
| 第二阶 | 15~25(含25)的部分 | 3.92 |
| 第三阶 | 25以上的得分 | n |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
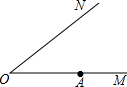 如图,已知ON是一条公路桥梁,现要在上游点A处再建一座与ON平行的大桥AB,请用尺规画出AB方向(不必写作法).并根据你的作法用一句话简单说明为什么AB和ON是平行的?
如图,已知ON是一条公路桥梁,现要在上游点A处再建一座与ON平行的大桥AB,请用尺规画出AB方向(不必写作法).并根据你的作法用一句话简单说明为什么AB和ON是平行的?查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,AD⊥BC于点D,点E在边AB上,CE与AD交于点G,EF⊥AD于点F,AE=5cm,BE=10cm,BD=9cm,CD=5cm,求AF、FG、GD的长.
如图,AD⊥BC于点D,点E在边AB上,CE与AD交于点G,EF⊥AD于点F,AE=5cm,BE=10cm,BD=9cm,CD=5cm,求AF、FG、GD的长.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com