
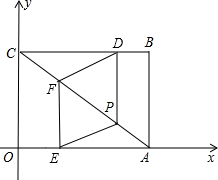
 ��ֱ������ϵ�У���OΪԭ�㣬��B������Ϊ��4��3�����ı���ABCO�Ǿ��Σ���D��B������ÿ��1����λ���ٶ����յ�C�˶���ͬʱ��E��O�������ÿ��1����λ���ٶ����յ�A�˶�����D��DP��BC��AC���ڵ�P����E��EF��AO��AC���ڵ�F������DF��PE��
��ֱ������ϵ�У���OΪԭ�㣬��B������Ϊ��4��3�����ı���ABCO�Ǿ��Σ���D��B������ÿ��1����λ���ٶ����յ�C�˶���ͬʱ��E��O�������ÿ��1����λ���ٶ����յ�A�˶�����D��DP��BC��AC���ڵ�P����E��EF��AO��AC���ڵ�F������DF��PE������ ��1���ɾ��ε����ʽ�ϵ�B�����꼴�ɵó���C��A�����꣬���ô���ϵ�����������ֱ��AC�Ľ���ʽ�������˶��Ĺ��ɵó���D�������ɴ˼��ɵó���P�����ꣻ
��2�������ܣ��ɵ�E������ɵó���F�����꣬�ɴ˵ó�DP=EF������DP��EF�ɵó��ı���EFDPΪƽ���ı��Σ��������ε����ʿɵó�DF=EF���ɴ˿ɵó�����t�ķ��̣��ⷽ�̼��ɵó����ۣ�
��3�����÷ָ�ͼ������������S�ı���COEP=S��COA-S��EPA�����������ε������ʽ���ɵó����ۣ��ٸ��ݶ��κ��������ʼ��ɽ����ֵ���⣻
��4���ɵ�A��E��P�����꣬�ɵó��߶�AE��EP��AP�ij��ȣ����ݵ��������ε����ʿɷ�����������ǣ�����������ȿɵó�����t�ķ��̣��ⷽ�̿ɵó�t��ֵ�������P�����м��ɵó����ۣ�
��� �⣺��1�����ı���ABCO�Ǿ��Σ���B������Ϊ��4��3����
���A��������4��0������C��������0��3����
��ֱ��AC�Ľ���ʽΪy=kx+3��
�ߵ�A��4��0����ֱ��AC�ϣ�
��0=4k+3=0����ã�k=-$\frac{3}{4}$��
��ֱ��AC�Ľ���ʽΪy=-$\frac{3}{4}$x+3��
�ߵ�D��B������ÿ��1����λ���ٶ����յ�C�˶���
���D��������4-t��3����
��DP��BC����P��ֱ��AC�ϣ�
���P��������4-t��-$\frac{3}{4}$��4-t��+3��������4-t��$\frac{3}{4}$t����0��t��4����
��2��������ԣ�
�ߵ�E��O�������ÿ��1����λ���ٶ����յ�A�˶���
���E��������t��0����
��EF��AO��
���F��������t��-$\frac{3}{4}$t+3����
��DP=3-$\frac{3}{4}$t��EF=3-$\frac{3}{4}$t��DF=$\sqrt{��4-2t��^{2}+[3-��3-\frac{3}{4}t��]^{2}}$��
��DP=EF��
��DP��BC��EF��AO��AO��BC��
��DP��EF��
���ı���EFDPΪƽ���ı��Σ�
���ı���EFDP�����Σ�
��DF=EF����$\sqrt{��4-2t��^{2}+[3-��3-\frac{3}{4}t��]^{2}}$=3-$\frac{3}{4}$t��
��ã�t=$\frac{7}{8}$����t=2����ȥ����
�ʵ�t��2ʱ���ı���EFDP����Ϊ���Σ���ʱt��ֵΪ$\frac{7}{8}$��
��3���ߵ�A��4��0������E��t��0����
��AE=4-t��
��S�ı���COEP=S��COA-S��EPA=$\frac{1}{2}$OC•OA-$\frac{1}{2}$AE•yP=6-$\frac{1}{2}$��4-t��$\frac{3}{4}$t=$\frac{3}{8}{t}^{2}$-$\frac{3}{2}$t+6��0��t��4����
��S�ı���COEP=$\frac{3}{8}{t}^{2}$-$\frac{3}{2}$t+6=$\frac{3}{8}$��t-2��2+$\frac{9}{2}$��
�൱t=2ʱ��S�ı���COEPȡ��Сֵ����СֵΪ$\frac{9}{2}$��
��4�������ܣ�
�ߵ�A��4��0������E��t��0������P��4-t��$\frac{3}{4}$t����
��AE=4-t��AP=$\frac{5}{4}$t��EP=$\sqrt{��4-2t��^{2}+[3-��3-\frac{3}{4}t��]^{2}}$��
��APE������������������
�ٵ�AE=APʱ����4-t=$\frac{5}{4}$t��
��ã�t=$\frac{16}{9}$��
��ʱ��P��$\frac{20}{9}$��$\frac{4}{3}$����
�ڵ�AE=EPʱ����4-t=$\sqrt{��4-2t��^{2}+[3-��3-\frac{3}{4}t��]^{2}}$��
��ã�t=0����ȥ������t=$\frac{128}{57}$��
��ʱ��P��$\frac{100}{57}$��$\frac{32}{19}$����
�۵�AP=EPʱ����$\frac{5}{4}$t=$\sqrt{��4-2t��^{2}+[3-��3-\frac{3}{4}t��]^{2}}$��
��ã�t=$\frac{4}{3}$����t=4����ȥ����
��ʱ��P��$\frac{8}{3}$��1����
���Ͽ�֪����APE��Ϊ���������Σ���ʱP�������Ϊ��$\frac{20}{9}$��$\frac{4}{3}$������$\frac{100}{57}$��$\frac{32}{19}$����$\frac{8}{3}$��1����
���� ���⿼���˾��ε����ʡ�����ϵ������������ʽ�������ľ��빫ʽ�Լ����ε����ʣ�����Ĺؼ��ǣ���1�����ô���ϵ�������ֱ��AC�Ľ���ʽ����2���������ε����ʵó�����t�ķ��̣���3�����÷ָ�ͼ����������ҳ�S����t�ĺ�����ϵʽ����4����������ۣ����������е��⣬�ѶȲ����Ϸ����������������Ŀʱ���ҳ�����������ô���ϵ���������������ʽ������һ�κ���ͼ���ϵ�������������ֱ���ϵ�������ǹؼ���


 ����С����ͬ������ϵ�д�
����С����ͬ������ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ������
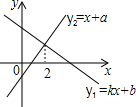 һ�κ���y1=kx+b��y2=x+a��ͼ����ͼ�������н��ۣ���k��0����a��0���۵�x��3ʱ��y1��y2�У���ȷ������Ǣ٣�
һ�κ���y1=kx+b��y2=x+a��ͼ����ͼ�������н��ۣ���k��0����a��0���۵�x��3ʱ��y1��y2�У���ȷ������Ǣ٣��鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
 ��ͼ����ƽ���ı���ABCD�У���E�DZ�AD���е㣬EC���Խ���BD�ڵ�F����EF��FC=1��2��
��ͼ����ƽ���ı���ABCD�У���E�DZ�AD���е㣬EC���Խ���BD�ڵ�F����EF��FC=1��2���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
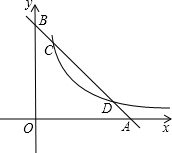 ��֪��һ�κ���y=-x+b��ͼ����x�ᡢy��Ľ���ֱ�ΪA��B�뷴��������$y=\frac{5}{x}��x��0��$��ͼ���ڵ�C��D����$\frac{BD}{BA}=\frac{2}{3}$��
��֪��һ�κ���y=-x+b��ͼ����x�ᡢy��Ľ���ֱ�ΪA��B�뷴��������$y=\frac{5}{x}��x��0��$��ͼ���ڵ�C��D����$\frac{BD}{BA}=\frac{2}{3}$���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� |  | B�� |  | C�� |  | D�� |  |
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com