
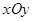 中,点
中,点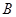 的坐标为
的坐标为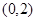 ,点
,点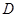 在
在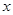 轴的正半轴上,
轴的正半轴上,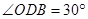 ,
,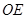 为△
为△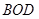 的中线,过
的中线,过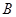 、
、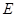 两点的抛物线
两点的抛物线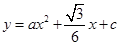 与
与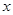 轴相交于
轴相交于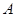 、
、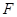 两点(
两点(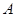 在
在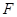 的左侧).
的左侧).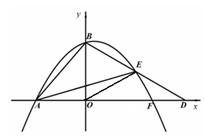
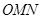 的顶点
的顶点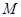 、
、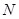 在线段
在线段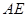 上,求
上,求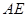 及
及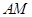 的长;
的长;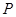 为△
为△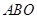 内的一个动点,设
内的一个动点,设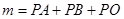 ,请直接写出
,请直接写出 的最小值,以及
的最小值,以及 取得最小值时,线段
取得最小值时,线段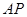 的长.
的长. 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源:不详 题型:解答题
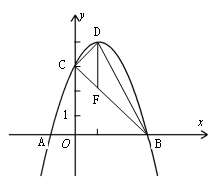
 轴,交直线BC于点F,求线段DF的长,并求△BCD的面积;
轴,交直线BC于点F,求线段DF的长,并求△BCD的面积;查看答案和解析>>
科目:初中数学 来源:不详 题型:解答题
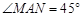 ,连结MC,NC,MN.
,连结MC,NC,MN.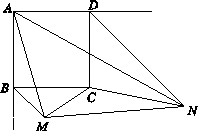
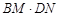 = ;(用含a的代数式表示)
= ;(用含a的代数式表示)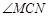 的度数;
的度数;查看答案和解析>>
科目:初中数学 来源:不详 题型:解答题

查看答案和解析>>
科目:初中数学 来源:不详 题型:解答题

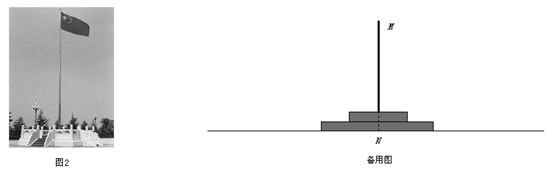
查看答案和解析>>
科目:初中数学 来源:不详 题型:解答题
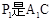 与AB的交点,点Q是
与AB的交点,点Q是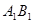 与BC的交点,求证:
与BC的交点,求证: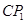 =
=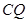 ;
;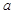 ,则CQ等于多少?
,则CQ等于多少?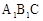 绕点C顺时针旋转到△
绕点C顺时针旋转到△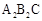 (如图3),点
(如图3),点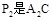 与AP1的交点.当旋转角为多少度时,有△A P1C∽△CP1P2? 这时线段
与AP1的交点.当旋转角为多少度时,有△A P1C∽△CP1P2? 这时线段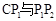 之间存在一个怎样的数量关系?.
之间存在一个怎样的数量关系?.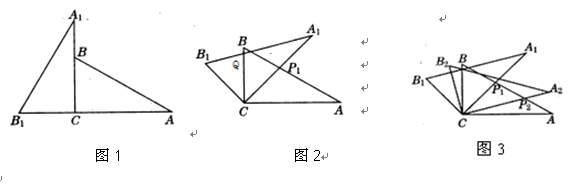
查看答案和解析>>
科目:初中数学 来源:不详 题型:单选题
 =
= ;③AC?BE=12;④3BF=4AC.其中结论正确的个数有( )
;③AC?BE=12;④3BF=4AC.其中结论正确的个数有( )
查看答案和解析>>
科目:初中数学 来源:不详 题型:解答题

 =BF.
=BF.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com