ĢĻ1ĢĐ
ĢĻ2ĢĐđýAŨũAEĄÍBCÓÚEĢŽđýDŨũDFĄÍBCÓÚFĢŽÔōËÄąßÐÎAEFDĘĮūØÐÎĢŪ
BE=CF=
=1ĢŪ
Öą―ĮČý―ĮÐÎCFDÖÐĢŽCF=1ĢŽCD=2ĢŽcosĄÏC=
ĄāĄÏC=60ĄãĢŽDF=
ĢŪ
ĄāĄÏABE=ĄÏC=60Ąã
ĄßQM
ĄÎAB
ĄāĄÏQMP=60Ąã
ĄßBM=tĢŽPF=ND=tĢŽFC=1ĢŽBC=4
ĄāPM=3-2tĢŽBP=3-tĢŪ
Öą―ĮČý―ĮÐÎQPMÖÐĢŽĄÏQMP=60ĄãĢŽPM=3-2tĢŽQP=
ĢĻ3-2tĢĐĢŪ
ĄßQPĄÍBCĢŽDFĄÍBC
ĄāQP
ĄÎDFĢŽ
ĄāĄũBQP
ĄŨĄũBDFĢŽ
Ąā
=
ĢŽžī
=
Ąā5t=6ĢŽžīt=1.2ĢĻsĢĐ
ĩąt=1.2sĘąĢŽQM
ĄÎAB
ĢĻ3ĢĐĩą0ĢžtĄÜ2ĘąĢŽČý―ĮÐÎBDFÖÐĢŽBF=3ĢŽDF=
ĢŽ
ĄāBD=2
Čý―ĮÐÎBCDÖÐĢŽCD=2ĢŽBD=2
ĢŽBC=4ĢŽ
ŌōīËBD
2+CD
2=BC
2ĢŽ
žīČý―ĮÐÎBDCĘĮÖą―ĮČý―ĮÐÎĢŽĮŌĄÏBDC=90ĄãĢŽĄÏDBC=30ĄãĢŪ
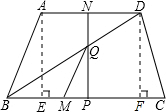
Öą―ĮČý―ĮÐÎBQPÖÐĢŽBP=3-tĢŽĄÏDBC=30ĄãĢŽ
ĄāPQ=
ĢĻ3-tĢĐ
ŌōīËĢšS=
ĄÁtĄÁ
ĢĻ3-tĢĐ=-
t
2+
t
ĩą2ĢžtĢž4ĘąĢŽÖą―ĮČý―ĮÐÎNBPÖÐĢŽĄÏABC=60ĄãĢŽBN=4-tĢŽ
ĄāBP=
ĢŪ
ÔÚÖą―ĮČý―ĮÐÎBPQÖÐĢŽĄÏDBC=30ĄãĢŽBP=
ĢŽ
ĄāQP=
ŌōīËĢšS=
ĄÁtĄÁ
=-
t
2+
t
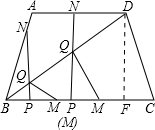
ĢĻ4ĢĐĩą0ĢžtĄÜ2ĘąĢŽžīNÔÚADÉÏĘąĢŽ·ÖÁ―ÖÖĮéŋö―øÐÐĖÖÂÛĢš
ĒŲĩąĄÏBMQ=90ĄãĢŽžīMÓëPĩãÖØšÏĢŽÄĮÃīBM+PF+CF=BM+ND+CF=2t+1=4
―âĩÃĢšt=1.5sĢŪ
ĒÚĩąĄÏBQM=90ĄãĢŽÔÚÖą―ĮČý―ĮÐÎNQDÖÐĢŽND=tĢŽĄÏADB=ĄÏDBC=30ĄãĢŽ
ĄāNQ=
tĢŪ
ĄßNP=
ĄāQP=
-
t
ÔÚÖą―ĮČý―ĮÐÎBQMÖÐĢŽĄÏDBC=30ĄãĢŽBM=t
ĄāQM=
t
ÔÚÖą―ĮČý―ĮÐÎQPMÖÐĢŽĄÏQMP=60ĄãĢŽQM=
t
ĄāQP=
t
Ąā
-
t=
tĢŪ
―âĩÃt=
sĢŪ
ĩą2ĢžtĢž4ĘąĢŽĄÏBQM=90Ąã
Öą―ĮČý―ĮÐÎBNPÖÐĢŽBN=4-tĢŽĄÏABC=60ĄãĢŽ
ĄāBP=
ĢŽ
ĄāPM=BM-BP=t-
=
ÔÚÖą―ĮČý―ĮÐÎBPQÖÐĢŽĄÏDBC=30ĄãĢŽBP=
ĄāPQ=
Öą―ĮČý―ĮÐÎQPMÖÐĢŽĄÏQMP=60ĄãĢŽPM=
ĄāPQ=
ŌōīË
=
ĢŽ
―âĩÃt=1.6sĢŽÓëīËĘątĩÄČĄÖĩ·ķΧēŧ·ûĢŽ
ŌōīËÕâÖÖĮéŋöēŧģÉÁĒĢŪ
ŨÛÉÏËųĘöĢŽĩąt=1.5sŧō
sĢŽĄũBMQĘĮÖą―ĮČý―ĮÐÎĢŪ

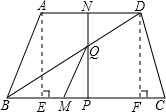
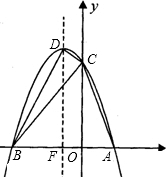
 ĩÄËŲķČÏōĩãBÔËķŊĢŪČôĩãMĄĒNÍŽĘąŋŠĘžÔËķŊĢŽÆäÖÐŌŧĩãĩ―īïÖÕĩãĢŽÁíŌŧĩãŌēÍĢÖđÔËķŊĢŽÔËķŊĘąžäΊtĢĻtĢū0ĢĐĢŪđýĩãNŨũNPĄÍBCÓëPĢŽ―ŧBDÓÚĩãQĢŪ
ĩÄËŲķČÏōĩãBÔËķŊĢŪČôĩãMĄĒNÍŽĘąŋŠĘžÔËķŊĢŽÆäÖÐŌŧĩãĩ―īïÖÕĩãĢŽÁíŌŧĩãŌēÍĢÖđÔËķŊĢŽÔËķŊĘąžäΊtĢĻtĢū0ĢĐĢŪđýĩãNŨũNPĄÍBCÓëPĢŽ―ŧBDÓÚĩãQĢŪ




 ÔÄķÁŋėģĩÏĩÁÐīð°ļ
ÔÄķÁŋėģĩÏĩÁÐīð°ļ
 A=45ĄãĢŽtanA=3Ģŧ
A=45ĄãĢŽtanA=3Ģŧ ÏßÓëxÖáĩÄÁíŌŧļö―ŧĩãĢŪ
ÏßÓëxÖáĩÄÁíŌŧļö―ŧĩãĢŪ