
(2006,旅顺)直线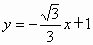 分别与x轴、y轴交于B、A两点.
分别与x轴、y轴交于B、A两点.
(1)求B、A两点的坐标;
(2)把△AOB以直线AB为轴翻折,点O落在平面上的点C处,以BC为一边作等边△BCD,求D点的坐标.
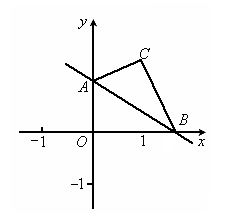
 学而优暑期衔接南京大学出版社系列答案
学而优暑期衔接南京大学出版社系列答案 Happy holiday欢乐假期暑假作业广东人民出版社系列答案
Happy holiday欢乐假期暑假作业广东人民出版社系列答案科目:初中数学 来源: 题型:
| b |
| 2a |
| 4ac-b2 |
| 4a |
查看答案和解析>>
科目:初中数学 来源: 题型:022
(2006,旅顺)某区从2 300名参加初中毕业升学统一考试数学测试的学生中随机抽取200名学生的试卷,成绩从低到高按59~89、90~199、120~134,135~150分成四组进行统计(最低成绩为59分,且分数均为整数),整理后绘出如图所示的各分数段频数分布直方图的一部分.已知前三个小组从左到右的频率依次为0.25,0.30,0.35.

(1)第四组的频数为________,并将频数颁布直方图补充完整;
(2)若90分及其以上成绩为及格,则此次测试中数学成绩及格以上(含及格)的人数约为________.
查看答案和解析>>
科目:初中数学 来源: 题型:044
(2006,旅顺)已知抛物线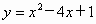 .将此抛物线沿x轴方向向左平移4个单位长度,得到一条新的抛物线.
.将此抛物线沿x轴方向向左平移4个单位长度,得到一条新的抛物线.
(1)求平移后的抛物线解析式;
(2)若直线y=m与这两条抛物线有且只有四个交点,求实数m的取值范围;
(3)若将已知的抛物线解析式改为了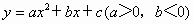 ,并将此抛物线沿x轴方向向左平移
,并将此抛物线沿x轴方向向左平移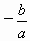 个单位长度,试探索问题(2).
个单位长度,试探索问题(2).
查看答案和解析>>
科目:初中数学 来源: 题型:044
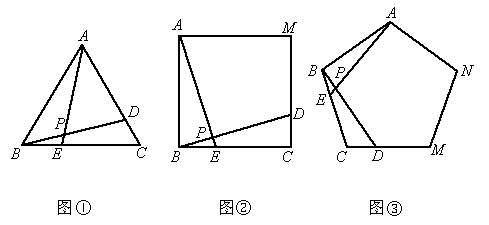
(2006,旅顺)如图①、②、③中,点E、D分别是正三角形ABC、正四边形ABCM、正五边形ABCMN中以C点为顶点的相邻两边上的点,且BE=CD,DB交AE于P点.
(1)求图①中,∠APD的度数;
(2)图②中,∠APD的度数为________,图③中,∠APD度数_________;
(3)根据前面探索,你能否将本题推广到一般的正n正形情况.若能,写出推广问题和结论;若不能,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com