
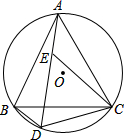
 如图,等边△ABC内接于⊙O,点D为
如图,等边△ABC内接于⊙O,点D为 |
| BC |

|


科目:初中数学 来源: 题型:
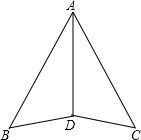 如图,∠B=∠C,AD平分∠BAC,求证:△ABD≌△ACD.若BD=3cm,则CD有多长?
如图,∠B=∠C,AD平分∠BAC,求证:△ABD≌△ACD.若BD=3cm,则CD有多长?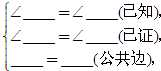
查看答案和解析>>
科目:初中数学 来源: 题型:
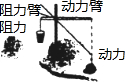 一杠杆装置如图,杆的一端拉起一物体,所受重力为300N.物体对杆的拉力的作用点到支点的杠长为1m.杠与水平线的倾斜角为45°,设在杠的另一端施加的压力为F(N),压力作用点到支点的距离为d(m)(杠杆自身的重量忽略不计).
一杠杆装置如图,杆的一端拉起一物体,所受重力为300N.物体对杆的拉力的作用点到支点的杠长为1m.杠与水平线的倾斜角为45°,设在杠的另一端施加的压力为F(N),压力作用点到支点的距离为d(m)(杠杆自身的重量忽略不计).查看答案和解析>>
科目:初中数学 来源: 题型:
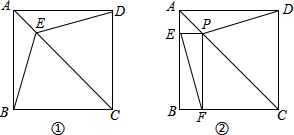 如图①,在正方形ABCD中,点E在AC上.
如图①,在正方形ABCD中,点E在AC上.查看答案和解析>>
科目:初中数学 来源: 题型:
 如图,在△ABC中,已知∠BAC=45°,AD⊥BC于点D,BD=2,DC=3,求AD的长.小萍同学灵活运用轴对称知识,将图形进行翻折变换,巧妙地解答了此题.请按照小萍的思路,探究并解答下列问题:
如图,在△ABC中,已知∠BAC=45°,AD⊥BC于点D,BD=2,DC=3,求AD的长.小萍同学灵活运用轴对称知识,将图形进行翻折变换,巧妙地解答了此题.请按照小萍的思路,探究并解答下列问题:查看答案和解析>>
科目:初中数学 来源: 题型:
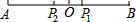 如图,已知线段AB,P1是AB的黄金分割点(AP1>BP1),点O是AB的中点,P2是P1关于点O的对称点.求证:P1B是P2B和P1P2的比例中项.
如图,已知线段AB,P1是AB的黄金分割点(AP1>BP1),点O是AB的中点,P2是P1关于点O的对称点.求证:P1B是P2B和P1P2的比例中项.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com