
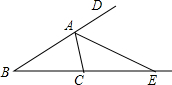
 已知:如图,在△ABC中,∠BAC的外角平分线与BC的延长线交于点E.求证:AB≠AC.
已知:如图,在△ABC中,∠BAC的外角平分线与BC的延长线交于点E.求证:AB≠AC. 分析 假设AB=AC,根据等腰三角形中等边对等角以及三角形的外角的性质证明∠ACB=∠CAE,则AE∥BC,与已知相矛盾,即可证得.
解答 证明:假设AB=AC.
∵AB=AC,
∴∠B=∠ACB,
又∵∠DAC=∠B+∠ACB,∠DAC=2∠DAE=2∠CAE,
∴∠ACB=∠CAE,
∴AE∥BC.与∠BAC的外角平分线与BC的延长线交于点E相矛盾.
则AB≠AC.
点评 本题结合角的比较考查反证法,解此题关键要懂得反证法的意义及步骤.
反证法的步骤是:
(1)假设结论不成立;
(2)从假设出发推出矛盾;
(3)假设不成立,则结论成立.
在假设结论不成立时要注意考虑结论的反面所有可能的情况,如果只有一种,那么否定一种就可以了,如果有多种情况,则必须一一否定.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
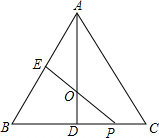 如图,在△ABC中,AB=AC=10,BC=12,D,E分别是边BC,AB的中点,AD平分EP,试判断以EP为直径的圆与直线AC的位置关系,并说明理由.
如图,在△ABC中,AB=AC=10,BC=12,D,E分别是边BC,AB的中点,AD平分EP,试判断以EP为直径的圆与直线AC的位置关系,并说明理由.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com