
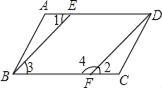
【题目】如图,已知AD∥BC,∠3+∠4=180°,要证∠1=∠2,请完善证明过程,并在括号内填上相应依据:
∵AD∥BC(已知)
∴∠l=∠3( ),
∵∠3+∠4=180°(已知),
∴BE∥DF( ),
∴ = ( ).
∴∠1=∠2( ).
 阳光试卷单元测试卷系列答案
阳光试卷单元测试卷系列答案科目:初中数学 来源: 题型:
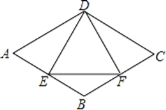
【题目】如图,在菱形ABCD中,E是AB边上一点,且∠A=∠EDF=60°,有下列结论:①AE=BF;②△DEF是等边三角形;③△BEF是等腰三角形;④∠ADE=∠BEF,其中结论正确的个数是( )
A.3
B.4
C.1
D.2
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】有大小两种货车,已知1辆大货车与3辆小货车一次可以运货14吨,2辆大货车与5辆小货车一次可以运货25吨.
(1)1辆大货车与1辆小货车一次可以运货各多少吨?
(2)1辆大货车一次费用为300元,1辆小货车一次费用为200元,要求两种货车共用10辆,两次完成80吨的运货任务,且总费用不超过5400元,有哪几种用车方案?请指出费用最低的一种方案,并求出相应的费用.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】元宵节将至,我校组织学生制作并选送50盏花灯,共包括传统花灯、创意花灯和现代花灯三大种.已知每盏传统花灯需要35元材料费,每盏创意花灯需要33元材料费,每盏现代花灯需要30元材料费.
(1)如果我校选送20盏现代花灯,已知传统花灯数量不少于5盏且总材料费不得超过1605元,请问选送传统花灯、创意花灯的数量有哪几种方案?
(2)当三种花灯材料总费用为1535元时,求选送传统花灯、创意花灯、现代花灯各几盏?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,AB=AC,AD平分∠BAC交BC于点D,分别过点A,D作AE∥BC,DE∥AB,AE与DE相交于点E,连结CE. 
(1)求证:AE=BD;
(2)求证:四边形ADCE是矩形.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知点A是反比例函数 ![]() 的图象上的一个动点,连接OA,若将线段O A绕点O顺时针旋转90°得到线段OB,则点B所在图象的函数表达式为 .
的图象上的一个动点,连接OA,若将线段O A绕点O顺时针旋转90°得到线段OB,则点B所在图象的函数表达式为 . 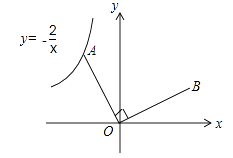
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一个四位数,记千位上和百位上的数字之和为x,十位上和个位上的数字之和为y,如果x=y,那么称这个四位数为“和平数”.
例如:2635,x=2+6,y=3+5,因为x=y,所以2635是“和平数”.
(1)请判断:3562 (填“是”或“不是”)“和平数”.
(2)直接写出:最小的“和平数”是 ,最大的“和平数”是 ;
(3)如果一个“和平数”的个位上的数字是千位上的数字的两倍,且百位上的数字与十位上的数字之和是14,求满足条件的所有“和平数”.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,∠1=∠2,G为AD的中点,BG的延长线交AC于点E,F为AB上的一点,CF与AD垂直,交AD于点H,则下面判断正确的有( )

①AD是△ABE的角平分线;②BE是△ABD的边AD上的中线;
③CH是△ACD的边AD上的高;④AH是△ACF的角平分线和高
A. 1个 B. 2个 C. 3个 D. 4个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,是直立在高速公路边水平地面上的交通警示牌,经测量得到如下数据:AM=4米,AB=8米,∠MAD=45°,∠MBC=30°,则警示牌的高CD为( )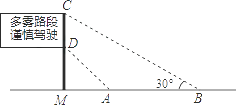
A.4 ![]() 米
米
B.(2 ![]() +2)米
+2)米
C.(4 ![]() ﹣4)米
﹣4)米
D.(4 ![]() ﹣4)米
﹣4)米
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com