练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情
    18．已知，一元二次方程x2-8x+15=0的两根分别是⊙O1和⊙O2的半径，当⊙O1和⊙O2相切时，O1O2的长度是（　　）
    A．2B．8C．2或8D．2＜O1O2＜8

    分析 先解方程求出⊙O1、⊙O2的半径，再分两圆外切和两圆内切两种情况讨论求解．

    解答 解：∵⊙O1、⊙O2的半径分别是方程x2-8x+15=0的两根，
    解得⊙O1、⊙O2的半径分别是3和5．
    ∴①当两圆外切时，圆心距O1O2=3+5=8；
    ②当两圆内切时，圆心距O1O2=5-3=2．
    故选C．

    点评 考查解一元二次方程-因式分解法和圆与圆的位置关系，同时考查综合应用能力及推理能力．注意：两圆相切，应考虑内切或外切两种情况是解本题的难点．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：填空题

    8．在实数1，-2，4，-$\sqrt{3}$中，最小的数是-2．

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

    9．算式2.5÷[（$\frac{1}{5}$-1）×（2+$\frac{1}{2}$）]之值为何？（　　）
    A．-$\frac{5}{4}$B．-$\frac{125}{16}$C．-25D．11

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

    6．下列计算正确的是（　　）
    A．3a2-6a2=-3B．（-2a）•（-a）=2a2C．10a10÷2a2=5a5D．-（a3）2=a6

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

    13．如图，四边形ABCD内接于⊙O，F是$\widehat{CD}$上一点，且$\widehat{DF}$=$\widehat{BC}$，连接CF并延长交AD的延长线于点E，连接AC．若∠ABC=105°，∠BAC=25°，则∠E的度数为（　　）
    A．45°B．50°C．55°D．60°

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

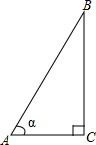    3．如图，为测量一棵与地面垂直的树BC的高度，在距离树的底端4米的A处，测得树顶B的仰角∠α=74°，则树BC的高度为（　　）
    A．$\frac{4}{tan74°}$米B．4sin74°米C．4tan74°米D．4cos74°米

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

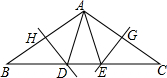    10．如图，在△ABC中，∠B=∠C=36°，AB的垂直平分线交BC于点D，交AB于点H，AC的垂直平分线交BC于点E，交AC于点G，连接AD，AE，则下列结论错误的是（　　）
    A．$\frac{BD}{BC}$=$\frac{\sqrt{5}-1}{2}$B．AD，AE将∠BAC三等分
    C．△ABE≌△ACDD．S△ADH=S△CEG

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    7．已知正方形ABCD，P为射线AB上的一点，以BP为边作正方形BPEF，使点F在线段CB的延长线上，连接EA、EC．

    （1）如图1，若点P在线段AB的延长线上，求证：EA=EC；
    （2）若点P在线段AB上．
    ①如图2，连接AC，当P为AB的中点时，判断△ACE的形状，并说明理由；
    ②如图3，设AB=a，BP=b，当EP平分∠AEC时，求a：b及∠AEC的度数．

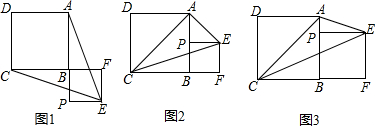
    查看答案和解析>>

    科目：初中数学 来源： 题型：填空题

    8．已知一个等腰三角形的两边长分别为2和4，则该等腰三角形的周长是10．

    查看答案和解析>>

    同步练习册答案